3.16. Mean Value Theorems for Riemann-Stieltjes Integrals

Theorem 3.25 (First Mean Value Theorem for Riemann-Stieltjes Integrals)

Assume \(\alpha\) is increasing on \([a, b]\) and \(f \in \mathfrak{R}(\alpha)\) on \([a, b]\). Let \(m = \inf_{x \in [a, b]}f(x)\) and \(M = \sup_{x \in [a, b]}f(x)\). Then there exists \(c \in [m, M]\) such that

\[\int_a^b f \dif\alpha = c \int_a^b \dif\alpha = c[\alpha(b) -\alpha(a)]\]

In particular, if \(f\) is continuous on \([a, b]\) then \(f\) can attain the value \(c\), i.e., exists \(x_0 \in [a, b]\) such that \(f(x_0) = c\).

Proof. If \(\alpha(a) = \alpha(b)\), then \(\alpha\) is constant and the integral evaluates to zero. In this case, simply choose \(c = f(a)\). Now, assume \(\alpha(a) < \alpha(b)\).

Because \(m \leq f(x) \leq M\)(regard \(m\) and \(M\) as constant functions) on \([a, b]\), applying the comparison theorem (Corollary 3.1), we have

\[\int_a^b m \dif\alpha\leq\int_a^b f \dif\alpha\leq\int_a^b M \dif\alpha\]

The number \(c\) defined by

\[c = \frac{1}{\alpha(b) - \alpha(a)}\int_a^b f \dif\alpha\]

is as desired.

Example 3.5

Consider \(f(x) = -x^2 + 2x + 3\) defined on \([0, 3]\). We have \(m = 0\) and \(M = 4\). The integral is \(\int_0^3 f(x) \dif x = 9\), which is represented by the blue area in Fig. 3.3.

Theorem 3.25 says that we can find a line \(y = c\) such that the area under \(y = c\) equals the area under \(f\) where \(0 = m \leq c \leq M = 4\). In this example, \(c = 3\). And because \(f\) is continuous, it attains the value \(c = 3\) on \([0, 3]\). Indeed, we have \(f(0) = f(2) = 3\).

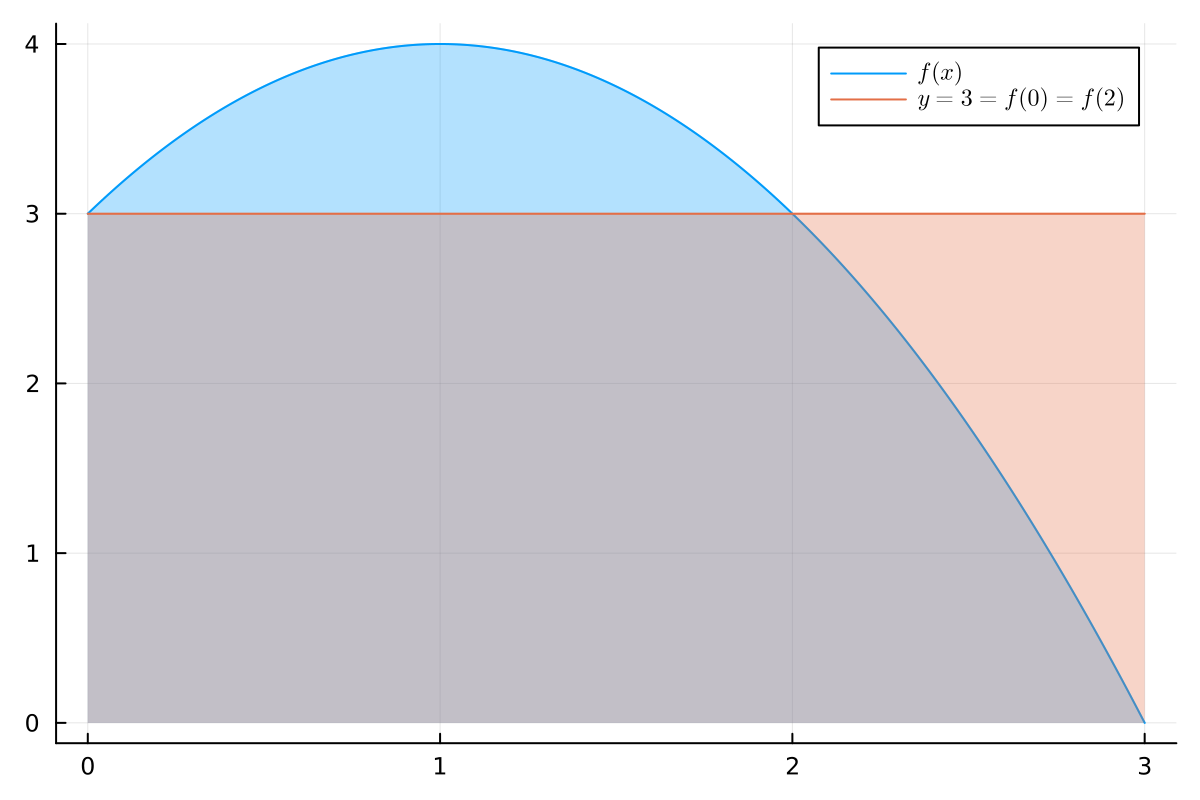
Fig. 3.3 The area under \(f\) equals the area under \(y = 3\).

Theorem 3.26 (Second Mean Value Theorem for Riemann-Stieltjes Integrals)

Assume \(\alpha\) is continuous and \(f\) is increasing on \([a, b]\), then there exists a point \(x_0 \in [a, b]\) such that

\[\int_a^b f \dif\alpha = f(a) \int_a^{x_0}\dif\alpha + f(b) \int_{x_0}^b \dif\alpha\]

The second mean value theorem can be proved easily using the first mean value theorem and integration by parts.

Proof. Because \(\alpha\) is continuous and \(f\) is increasing, it is clear that \(f \in \mathfrak{R}(\alpha)\) on \([a, b]\) and, of course, \(\alpha \in \mathfrak{R}(f)\) on \([a, b]\).

Applying the first mean value theorem (Theorem 3.25), we have

(3.43)\[\int_a^b \alpha\dif f = \alpha(x_0) [f(b) - f(a)]\]

for some \(x_0 \in [a, b]\). On the other hand, by the theorem of integration by parts, we have

(3.44)\[\int_a^b f \dif\alpha + \int_a^b \alpha\dif f = f(b) \alpha(b) - f(a) \alpha(a)\]

Combining (3.43) and (3.44), we obtain that

\[\begin{split}\int_a^b f \dif\alpha& = f(b) \alpha(b) - f(a) \alpha(a) - f(b) \alpha(x_0) + f(a) \alpha(x_0) \\& = f(a)[\alpha(x_0) - \alpha(a)] + f(b)[\alpha(b) - \alpha(x_0)]\\& = f(a) \int_a^{x_0}\dif\alpha + f(b) \int_{x_0}^b \dif\alpha\end{split}\]

which is as desired.

Example 3.6

For Riemann integrals, we can interpret Theorem 3.26 as follows. For example, consider \(f(x) = 2 - \cos(x), \; x \in [0, \pi]\). By the second mean value theorem, we can find a point \(x_0 \in [0, \pi]\)(in this case, \(x_0 = \pi / 2\)) such that the area under \(f\) is equal to the sum of areas of two rectangles. One rectangle has width \(x_0 - a = \pi/2 - 0\) and height \(f(a) = f(0)\). And the other one has width \(b - x_0=\pi - \pi/2\) and height \(f(b) = f(\pi)\). See Fig. 3.4 for an illustration.

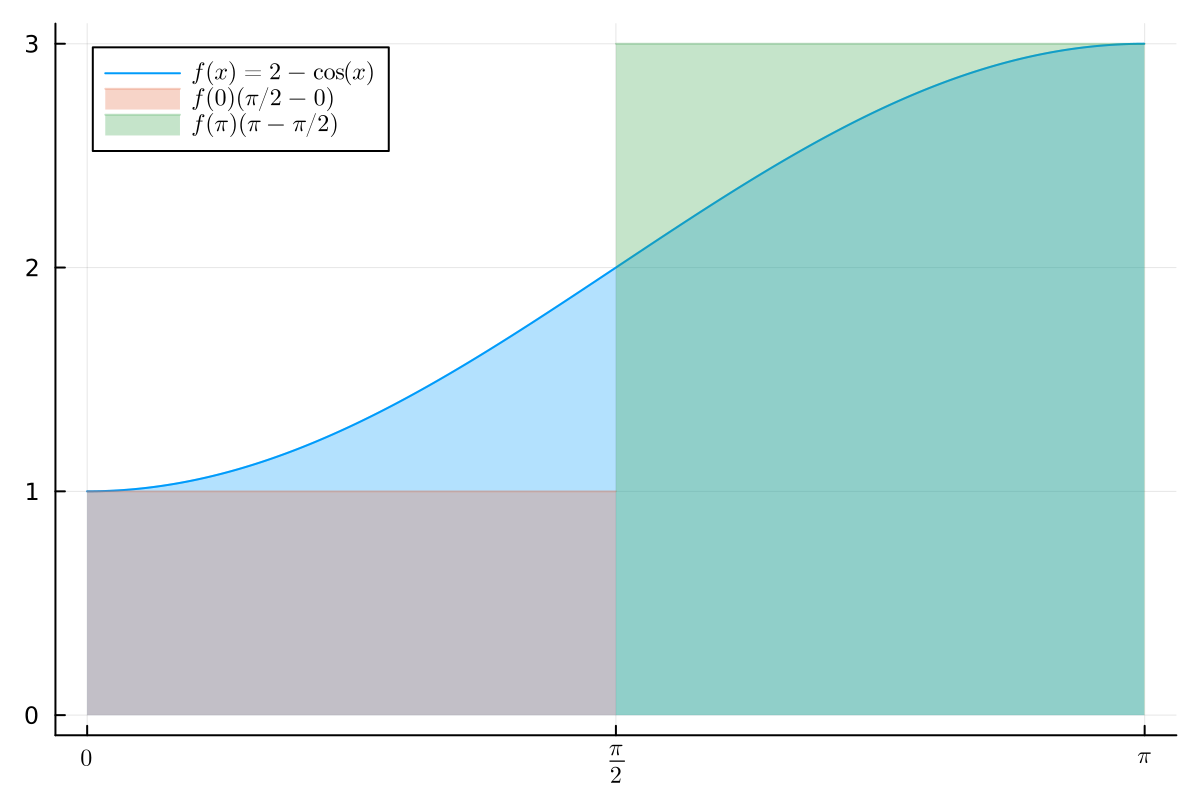
Fig. 3.4 The area under \(f\) can be decomposed of two rectangles.