2.2. Total Variation

Recall that \(f\) is said to be of bounded of variation on \([a, b]\) if, equivalently to what we stated, the set

(2.2)\[\set{\sum_{k=1}^n \abs{\Delta f_k}}{P \in \CALP[a, b]}\]

or with our shortened notation

\[\set{v(P, f)}{P \in \CALP[a, b]}\]

is bounded above. This set is of course nonempty for \(\{a, b\}\) is clearly a partition. By the least upper bound property, the set in (2.2) has a supremum, which is referred to as total variation of \(f\) on \([a, b]\).

Definition 2.3

Let \(f\) be of bounded variation on \([a, b]\). The total variation, denoted by \(V_a^b (f)\), of \(f\) on \([a, b]\) is defined as

\[V_a^b (f) := \sup_{P \in \CALP[a, b]} v(P, f) = \sup\set{\sum_{k=1}^n \abs{\Delta f_k}}{P \in \CALP[a, b]}\]

Note

We adopt the notation \(V_a^b(f)\), which is inspired by the notion of a definite integral \(\int_a^b f(x) \dif x\). And as we shall see, these two concepts indeed share some similar properties, namely, the linear properties.

Notations are very important for they provide intuitive expressions of the intrinsic mathematical concepts.

From this definition, we have some simple observations. First, the value of \(V_a^b (f)\) is nonnegative. And it is easy to prove that \(V_a^b (f) = 0\) if and only if \(f\) is constant on \([a, b]\).

The simplest function of bounded variation (well, apart from a constant function) is monotonic function. It is natural to ask what is its total variation. With a little thought, one can imagine that it should be the absolute value of the difference at the endpoints.

Proposition 2.5

If \(f\) is a monotonic function on \([a, b]\), then its total variation is the absolute value of the difference of the function values at the endpoints, i.e.,

\[V_a^b(f) = \abs{f(a) - f(b)}\]

Proof. We only prove the case that \(f\) is increasing. For any partition \(P = \{x_0, \dots, x_n\}\) of \([a, b]\), we have

\[\sum_{k=1}^n \abs{f(x_k) - f(x_{k-1})} = \sum_{k=1}^n [f(x_k) - f(x_{k-1})] = f(b) - f(a) \]

Note that the sum is independent of the partition. Hence, the set in (2.2) is just a constant. Therefore, the total variation \(V_a^b(f) = f(b) - f(a)\).

When studying functions of bounded variation, in most cases, we are often interested in monotonic functions or continuous and differentiable functions. (Proposition 2.2 and Proposition 2.3.)

Note

On one hand, we will see in Theorem 2.5, a function is of bounded variation if and only if it can be expressed as a difference of two increasing functions, the need of studying monotonic functions arises naturally.

On the other hand, as we shall see in the chapter on Riemann-Stieltjes integrals, we assume the integrator \(\alpha\) is of bounded variation. Since integrator \(\alpha\) will be put after the differential operator, \(\dif \alpha\), and we often hope to express it as \(\alpha^\prime(t) \dif t\) to reduce the integral to Riemann integral and compute its value, we would like \(\alpha\) to be differentiable.

But if we are curious about whether some piecewise functions are of bounded variation, then Proposition 2.2 and Proposition 2.3 will not be enough.

Example 2.4

For example, consider the following function defined on \([0, 3]\):

\[\begin{split}f(x) = \begin{cases} x, & 0 \leq x \leq 1 \\ -(x-1)(x-3), & 1 < x \leq 3 \end{cases}\end{split}\]

Fig. 2.3 depicts its graph.

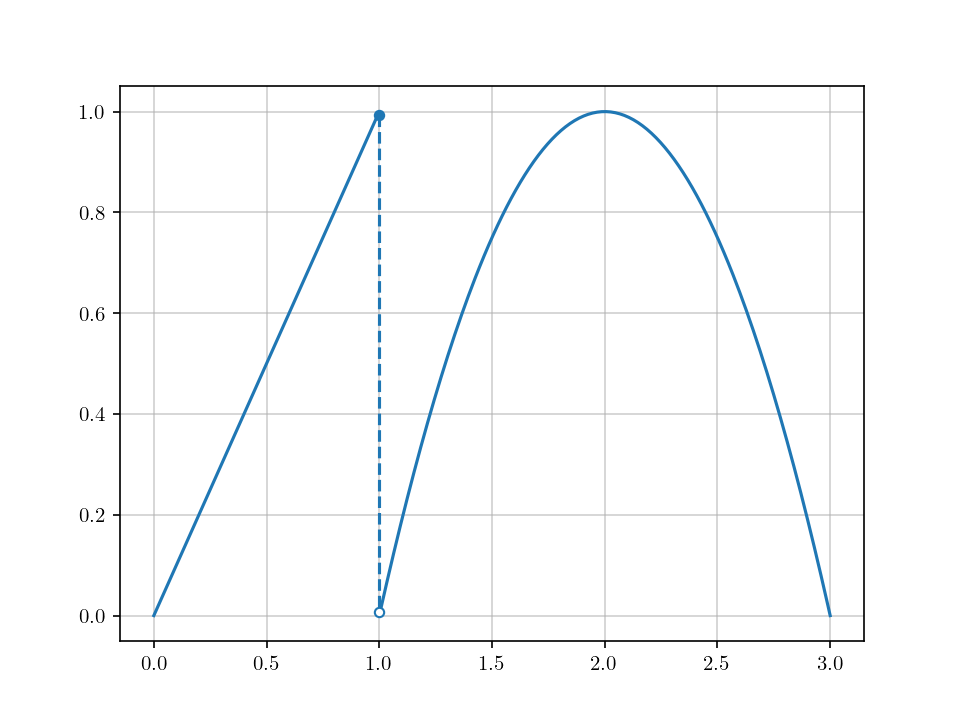
Fig. 2.3 Is this function of bounded variation on \([0, 3]\)?

Intuitively, the function in Fig. 2.3 should be of bounded variation. But we must be careful about the jump point, which we have not covered in the previous discussion.

Proposition 2.6

Suppose \(f\) is of bounded variation on \([a, b]\), and is continuous at \(x = a\). If function \(g\) is defined by revising the value at \(x=a\), i.e.,

\[\begin{split}g(x) = \begin{cases} f(x), & x \in (a, b] \\ y, & x = a \end{cases}\end{split}\]

then \(g\) is still of bounded variation on \([a, b]\). And its total variation is given by

\[V_a^b(g) = V_a^b(f) + \abs{y - f(a)}\]

Proof. Let \(P\) be a partition of \([a, b]\). We have

(2.3)\[\begin{split}v(P, g) & = \abs{g(x_1) - g(a)} + \cdots\abs{g(x_n) - g(x_{n-1})}\nonumber\\& = \abs{f(x_1) - y} + \cdots\abs{f(x_n) - f(x_{n-1})}\nonumber\\& \leq\left[\abs{y - f(a)} + \abs{f(x_1) - f(a)}\right] + \cdots\abs{f(x_n) - f(x_{n-1})}\nonumber\\& = \abs{y - f(a)} + v(P, f) \nonumber\\& \leq\abs{y - f(a)} + V_a^b(f)\end{split}\]

This shows that \(g\) is of bounded variation on \([a, b]\).

Now, we compute its total variation. Let \(\varepsilon > 0\) be arbitrary. Because \(f\) is continuous at \(x=a\), there exists \(\delta > 0\) such that

\[\abs{x - a} < \delta\implies\abs{f(x) - f(a)} < \varepsilon/4 \]

By the definition of total variation and Proposition 2.4, there exists a fine enough partition \(P\) such that the minimum length of the subinterval is less than \(\delta\), and

\[v(P, f) > V_a^b(f) - \varepsilon/2 \]

On the subinterval \([a=x_0, x_1]\), we have

\[\begin{split}\abs{\Delta g_1}& = \abs{g(x_1) - g(x_0)}\\& = \abs{f(x_1) - y}\\& \geq\abs{f(a) - y} - \abs{f(x_1) - f(a)}\\& = \abs{f(a) - y} + \abs{f(x_1) - f(a)} - 2\abs{f(x_1) - f(a)}\\& \text{Note that $\abs{x_1 - x_0} < \delta$, hence we may estimate the last term as follows}\\& > \abs{f(a) - y} + \abs{f(x_1) - f(a)} - 2 \cdot\varepsilon/4 \\& > \abs{f(a) - y} + \abs{f(x_1) - f(a)} - \varepsilon/2 \end{split}\]

Note

When reaching

\[\abs{\Delta g_1}\geq\abs{f(a) - y} - \abs{f(x_1) - f(a)}\]

in the above derivation, one may be worried that it is not proceeding towards the goal since we have a minus sign before \(\abs{f(x_1) - f(a)}\). But since this term \(\abs{f(x_1) - f(a)}\) can be made arbitrarily small, we can always add it (to construct the sum \(v(P, f)\)) and then subtract it, and make the trailing negative term \(-2\abs{f(x_1) - f(a)}\) negligible, as what we did above.

It then follows that

\[v(P, g) > \abs{f(a) - y} + v(P, f) - \varepsilon/2 > \abs{f(a) - y} + V_a^b(f) - \varepsilon\]

Therefore, we have

\[V_a^b(g) \geq v(P, g) \geq\abs{f(a) - y} + V_a^b(f) \]

Compare this to (2.3), we may conclude

\[V_a^b(g) = V_a^b(f) + \abs{f(a) - y}\]

The function \(f\) in Example 2.4 can be regarded as a sum of two functions on \([0, 3]\), \(f(x) = g(x) + h(x)\) where

\[\begin{split}g(x) & = \begin{cases} x, & x \in [0, 1] \\ 0, & x \in (1, 3] \end{cases}& & = (x \mapsto x) \ind_{[0, 1]}\\ h(x) & = \begin{cases} 0, & x \in [0, 1) \\ \tilde{h}(x), & x \in [1, 3] \end{cases}& & = \tilde{h}\ind_{[1, 3]}\end{split}\]

where

\[\begin{split}\tilde{h}(x) = \begin{cases} -(x-1)(x-3), & x \in (1, 3] \\ 0, & x = 1 \end{cases}\end{split}\]

We have already seen that functions like \(\tilde{h}\) are of bounded variation in Proposition 2.6. If we know the sum of two functions of bounded variation (on the same interval) is also of bounded variation (Theorem 2.1), we may then conclude that piecewise functions like \(f\) in Example 2.4 are indeed of bounded variation.

Hence, the next step to do is studying whether functions like \(g\) and \(h\) are of bounded variation. Describing in words, such functions are constructed by extending a function of bounded variation to a larger interval by defining function values of everywhere else in the larger interval to be zeros.

Theorem 2.1

Let \(f\) and \(g\) be of bounded variation on \([a, b]\), then so are their sum, difference and product. Moreover, we have the following inequalities:

(2.4)\[V_a^b (f \pm g) \leq V_a^b (f) + V_a^b (g)\]

and

(2.5)\[V_a^b (fg) \leq\sup_{x \in [a, b]}\abs{g(x)} V_a^b (f) + \sup_{x \in [a, b]}\abs{f(x)} V_a^b (g)\]

Note

Note that the supremums in (2.5) indeed exist since the functions \(f\) and \(g\) are bounded due to Proposition 2.1.

Proof. We first show that the sum and the difference of two functions are of bounded variation, and satisfy (2.4). Let \(P\) be an arbitrary partition of \([a, b]\). On each subinterval, we have

\[\begin{split}\abs{\Delta (f \pm g)_k}& = \abs{f(x_{k}) \pm g(x_{k}) - [f(x_{k-1}) \pm g(x_{k-1})]}\\& = \abs{\Delta f_k \pm \Delta g_k}\\& \leq\abs{\Delta f_k} + \abs{\Delta g_k}\end{split}\]

Taking the sum over \(k\), we have

\[\sum_{k}\abs{\Delta (f \pm g)_k}\leq\sum_{k}\abs{\Delta f_k} + \sum_k \abs{\Delta g_k}\leq V_a^b (f) + V_a^b (g) \]

The above inequality shows that \(f \pm g\) is of bounded variation on \([a, b]\), and (2.4) is satisfied.

In the following, we show that the product of two Functions are of bounded variation and satisfies (2.5). Let \(P\) be an arbitrary partition of \([a, b]\). On each subinterval, we have

\[\begin{split}\abs{\Delta (fg)_k}& = \abs{f(x_{k}) g(x_{k}) - f(x_{k-1}) g(x_{k-1})}\\& \text{Add and subtract the term $f(x_{k-1})g(x_{k})$}\\& = \abs{ g(x_{k})[ f(x_{k}) - f(x_{k-1})] + f(x_{k-1})[ g(x_{k}) - g(x_{k-1}) ] }\\& \leq\abs{g(x_{k})}\abs{\Delta f_k} + \abs{f(x_{k-1})}\abs{ \Delta g_k }\\& \leq\sup_{x \in [a, b]}\abs{g(x)}\abs{\Delta f_k} + \sup_{x \in [a, b]}\abs{f(x)}\abs{\Delta g_k}\end{split}\]

Summing over \(k\), we have

\[\begin{split}\sum_k \abs{\Delta (fg)_k}\leq\sup_{x \in [a, b]}\abs{g(x)}\sum_k \abs{\Delta f_k} + \sup_{x \in [a, b]}\abs{f(x)}\sum_k \abs{\Delta g_k}\\\leq\sup_{x \in [a, b]}\abs{g(x)} V_a^b (f) + \sup_{x \in [a, b]}\abs{f(x)} V_a^b (g) \end{split}\]

This shows the product \(fg\) is in fact of bounded variation on \([a, b]\), and (2.5) is satisfied.

We must exclude the quotients from the above theorem since the reciprocal \(\frac{1}{f}\) of \(f\) may not be of bounded variation even though \(f\) is.

Example 2.5

Consider function

\[\begin{split}f(x) = \begin{cases} 1-x, & 0 \leq x < 1 \\ -x, & 1 \leq x \leq 2 \end{cases}\end{split}\]

Function \(f\) is of bounded variation on \([0, 2]\) since it is decreasing. Its reciprocal is

\[\begin{split}\frac{1}{f(x)} = \begin{cases} \frac{1}{1-x}, & 0 \leq x < 1 \\ -\frac{1}{x}, & 1 \leq x \leq 2 \end{cases}\end{split}\]

Figure Fig. 2.4 depicts the graphs of \(f\) and \(\frac{1}{f}\).

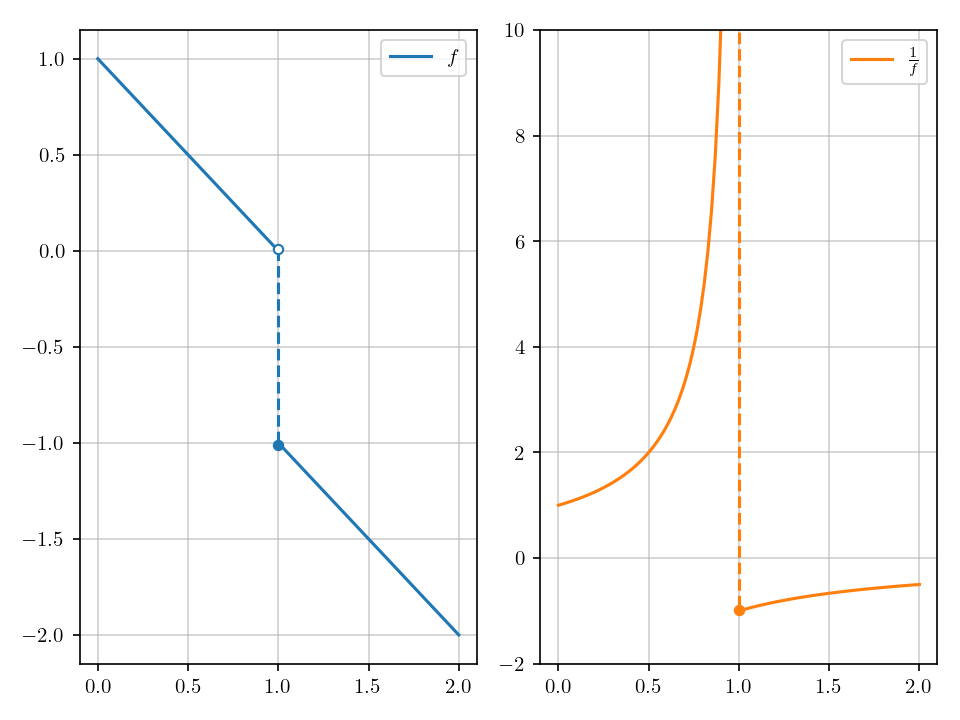
Fig. 2.4 Left: \(f\) is of bounded variation for it is decreasing. Right: \(\frac{1}{f}\) is not of bounded variation for it is unbounded.

Note that \(\frac{1}{f}\) goes to positive infinity when \(x \to 1^-\). Therefore, by Proposition 2.1, \(\frac{1}{f}\) is not of bounded variation on \([0, 2]\) since it is not bounded.

To extend Theorem 2.1 to quotients, we need to required that \(f\) is bounded away from zero in the interval.

Theorem 2.2

Let \(f\) be of bounded variation on \([a, b]\). And there exists \(m > 0\) such that \(f(x) \geq m\) for all \(x \in [a, b]\). Then the reciprocal of \(f\) is of bounded variation on \([a, b]\), and

\[V_a^b ( \frac{1}{f}) \leq\frac{1}{m^2} V_a^b (f) \]

Proof. Let \(P\) be any partition of \([a, b]\). On each subinterval \([x_{k-1}, x_k]\), we have

\[\begin{split}\abs{\Delta (\frac{1}{f})_k}& = \abs{\frac{1}{f(x_k)} - \frac{1}{f(x_{k-1})}}\\& = \abs{\frac{\Delta f_k}{f(x_{k-1}) f(x_k)}}\\& \leq\frac{\abs{ \Delta f_k }}{m^2}\end{split}\]

Summing over \(k\), we have

\[\sum_k \abs{\Delta (\frac{1}{f})_k}\leq\frac{1}{m^2}\sum_k \abs{\Delta f_k}\leq\frac{1}{m^2} V_a^b (f) \]

Therefore, \(\frac{1}{f}\) is of bounded variation on \([a, b]\).

2.2.1. Additive Property of Total Variation

Theorem 2.3

Let \(f\) be of bounded variation on \([a, b]\), and \(c \in (a, b)\). Then \(f\) is of bounded variation on the subintervals \([c, b]\) and \([a, c]\). Moreover, we have

(2.6)\[V_a^b(f) = V_a^c(f) + V_c^b(f)\]

Proof. We will first show that \(f\) is of bounded variation on each subinterval, and

(2.7)\[V_a^c(f) + V_c^b(f) \leq V_a^b(f)\]

Let \(P^\prime\) and \(P^{\prime\prime}\) be partitions of \([a, c]\) and \([c, b]\), respectively, and let \(P = P^\prime \cup P^{\prime\prime}\). Note that \(P\) is a partition of \([a, b]\), and by reviewing the notation of \(v(P, f)\) one may easily conclude that \(v(P^\prime, f) + v(P^{\prime\prime}, f) = v(P, f)\). Since \(f\) is of bounded of variation on \([a, b]\), we have

(2.8)\[v(P^\prime, f) + v(P^{\prime\prime}, f) = v(P, f) \leq V_a^b (f)\]

The above inequality holds for any partition \(p^\prime\) of \([a, c]\) and any partition \(P^{\prime\prime}\) of \([c, b]\). Therefore, by definition, \(f\) is of bounded variation on \([a, c]\) and \([c, b]\). Moreover, taking the supremum over \(P^\prime\) and then over \(P^{\prime\prime}\) on both sides of (2.8), we will obtain exactly (2.7).

To show the equality (2.6), we also need to show

(2.9)\[V_a^c(f) + V_c^b(f) \geq V_a^b (f)\]

Let \(\varepsilon > 0\) be arbitrary. There exists a partition \(P\) of \([a, b]\) such that \(v(P, f) > V_a^b(f) - \varepsilon\). Let

\[P^\prime = ( P \cap[a, c]) \cup\{c\}\quad\text{and}\quad P^{\prime\prime} = ( P \cap[c, b]) \cup\{c\}\]

It is clear that \(P^\prime\) and \(P^{\prime\prime}\) are partitions of \([a, c]\) and \([c, b]\), respectively. By Proposition 2.4, we have

(2.10)\[V_a^c(f) + V_c^b(f) \geq v(P^\prime, f) + v(P^{\prime\prime}, f) \geq v(P, f) > V_a^b(f) - \varepsilon\]

Because (2.10) holds for every \(\varepsilon > 0\), (2.9) is proved.

Applying the above theorem, we can immediately conclude that \(f\) is also of bounded variation on any interval contained in \([a, b]\).

Corollary 2.1

If \(f\) is of bounded variation on \([a, b]\), and \([c, d] \subseteq[a, b]\), then \(f\) is also of bounded variation on \([c, d]\).

Proof. With the given condition, we have \(a \leq c < d \leq b\). If \(c = a\) or \(d = b\), then the assumption of this corollary reduces to the one in Theorem 2.3.

Now, we assume that \(a < c < d <b\). Regarding \(c\) as an intermediate point in \([a, b]\), Theorem 2.3 shows that \(f\) is of bounded variation on \([c, b]\). Next, because \(d \in (c, b)\), applying Theorem 2.3 again, we conclude that \(f\) is of bounded variation on \([c, d]\).

2.2.2. Total Variation as a Function of the Right Endpoint

Suppose \(f\) is of bounded variation on \([a, b]\). For any \(x \in (a, b)\). Theorem 2.3 tells us that \(f\) is of bounded variation on \([a, x]\). Therefore, we can regard \(V_a^x (f)\) as a function of \(x\).

Note

This is very similar to considering \(\int_a^x f(t) \dif t\) as a function of the upper limit of the integral, which again shows that our notation of the total variation rather helpful.

When \(x = b\), it is just the total variation of \(f\) on the entire interval. We don’t have definition for \(x = a\) yet. But we can easily fix this by naturally defining \(V_a^a (f) := 0\). Now, function \(V_a^x(f)\) is defined on the entire interval \([a, b]\).

In the next chapter, we will study the Riemann-Stieltjes integral, which is more generalized definition of the Riemann integral. In the texts of the Riemann-Stieltjes integral \(\int_a^b f \dif \alpha\), we often assume that the integrator \(\alpha\) is increasing (or slightly more generalized, monotonic)[Rudin, 1976]. But we can extend the results easily to a even more general assumption that the integrator \(\alpha\) is of bounded variation on \([a, b]\).

The key of achieving this is that a function of bounded variation can be written as a difference of two increasing functions, and conversely, the difference of two increasing functions is of bounded variation (Theorem 2.5). And the following theorem tells us exactly how to find such increasing functions.

Theorem 2.4

Let \(f\) be of bounded variation on \([a, b]\). Then

1. \(V_a^x(f)\) is increasing on \([a, b]\), and

2. \(V_a^x(f) - f(x)\) is also increasing.

Proof. Let \(h > 0\)(and \(x + h \leq b\)), by Theorem 2.3, we have

\[V_a^x (f) + V_x^{x+h}(f) = V_a^{x+h}(f) \]

Note

We have seen in Corollary 2.1 that \(V_x^{x+h}(f)\) indeed exists.

It then follows that

\[V_a^{x+h}(f) - V_a^{x}(f) = V_x^{x+h}(f) \geq 0 \]

This shows \(V_a^x(f)\) is increasing.

Next, we will prove \(V_a^x(f) - f(x)\) is creasing. To ease the notation, let \(g(x) = V_a^x(f) - f(x)\). Similarly, suppose \(h > 0\) and \(x + h \leq b\), consider the difference

(2.11)\[g(x+h) - g(x) = V_x^{x+h}(f) + [f(x+h) - f(x)]\]

Note

Seeing the term \(f(x+h) - f(x)\) in the context of total variation, we immediately think of the partition \(P = \{x, x+h\}\) of \([x, x+h]\).

We have

\[\abs{f(x+h) - f(x)}\leq V_x^{x+h}(f) \]

It then follows that

\[V_x^{x+h}(f) \geq\abs{f(x+h) - f(x)}\geq -[f(x+h) - f(x)]\]

which further implies

(2.12)\[V_x^{x+h}(f) + [f(x+h) - f(x)]\geq 0\]

Comparing (2.11) and (2.12), we conclude that \(g(x)\) is indeed increasing.

2.2.3. Characterization of Functions of Bounded Variation

With the help of Theorem 2.4, we can easily prove the following elegant theorem, which characterizes functions of bounded variation. It states that a function on \([a, b]\) is of bounded variation if and only if it can be written as a difference of two increasing functions. The difficult part of find such increasing functions is already handled by Theorem 2.4.

Theorem 2.5

Let \(f\) be defined on \([a, b]\), then \(f\) is of bounded variation if and only if it can be expressed as a difference of two increasing functions.

Proof. We first suppose that \(f\) is of bounded variation. Then Theorem 2.4 shows that \(V_a^x(f)\) and \(V_a^x(f) - f(x)\) are both increasing on \([a, b]\). Since we can write

\[f(x) = V_a^x(f) - [ V_a^x (f) - f(x)]\]

It is proved.

Reversely, suppose that \(f\) can be expressed as a difference of two increasing functions \(g\) and \(h\) on \([a, b]\), \(f = g - h\). Proposition 2.2 tells us that \(g\) and \(h\) are of bounded variation since they are increasing functions. Then by Theorem 2.1, we know that \(g - h\) is also of bounded variation. This completes the proof.

Note

We can also make these two increasing functions strict. Suppose \(f = g - h\). We can easily achieve this by defining \(\tilde{g}(x) = g(x) + x\) and \(\tilde{h}(x) = h(x) + x\).