2.1. Functions of Bounded Variation

Definition 2.1

Let \([a, b]\) be an interval. A set of points

\[P = \{ x_0, x_1, \dots, x_n \}\]

satisfying

\[a = x_0 < x_1 < \cdots < x_n = b \]

is called a partition of \([a, b]\).

The interval \([x_{k-1}, x_k]\) is called the \(k\)-th subinterval of \(P\), and we often write \(\Delta x_k = x_k - x_{k-1}\).

The collection of all partitions of \([a, b]\) is denoted by \(\CALP[a, b]\).

Note

In mathematics texts, we have another definition of partitions, which states that a partition of a set \(S\) is a collection of subsets of \(S\) such that they are disjoint and their union equals \(S\). We should not confuse these two definitions.

Definition 2.2

Let \(f\) be a real-valued function on \([a, b]\). If \(P = \{x_0, \dots x_n\}\) is a partition of \([a, b]\), write \(\Delta f_k = f(x_k) - f(x_{k-1})\). If there exists a positive number \(M\) such that

(2.1)\[\sum_{k=1}^n \abs{\Delta f_k}\leq M \]

for all partitions \(P\) of \([a, b]\), then we say that \(f\) is of bounded variation on \([a, b]\).

Note

A geometric interpretation of the sum \(\sum_{k=1}^n \abs{\Delta f_k}\) is the total vertical length of several pieces of the function. Imagine a point moving along the curve of the function from the left to the right. If the partition gets finer and finer, then \(\sum_{k=1}^n \abs{\Delta f_k}\) will become the length of its journey projected on the \(y\)-axis. In fact, it is defined as the total variation as we shall introduce later.

Sometimes, it is convenient to denote the sum \(\sum_{k=1}^n \abs{\Delta f_k}\) by the symbol

\[v(P, f) := \sum_{k=1}^n \abs{\Delta f_k}\]

We do not use the capital letter \(V\) here for it is reserved for the total variation.

A simple observation is that a function of bounded variation is also bounded.

Proposition 2.1

Let \(f\) be a function of bounded variation on \([a, b]\). Then \(f\) is bounded on \([a, b]\).

Proof. By definition, there exists \(M > 0\) such that (2.1) holds for any partitions of \([a, b]\). For any \(x \in (a, b)\), consider the partition \(P = \{a, x, b\}\). We have

\[\abs{f(x) - f(a)} + \abs{f(b) - f(x)}\leq M \]

This implies that \(\abs{f(x) - f(a)} \leq M\), which further implies \(\abs{f(x)} \leq \abs{f(a)} + M\). Note that \(x\) is arbitrarily chosen from \((a, b)\). Therefore, \(f\) is indeed bounded on \([a, b]\).

But a bounded function is not necessarily of bounded variation.

Example 2.1

Consider the function

\[\begin{split}f(x) = \begin{cases} \cos \frac{1}{x}, & x \in (0, 1] \\ 0, & x = 0 \end{cases}\end{split}\]

Its graph is shown in Fig. 2.1.

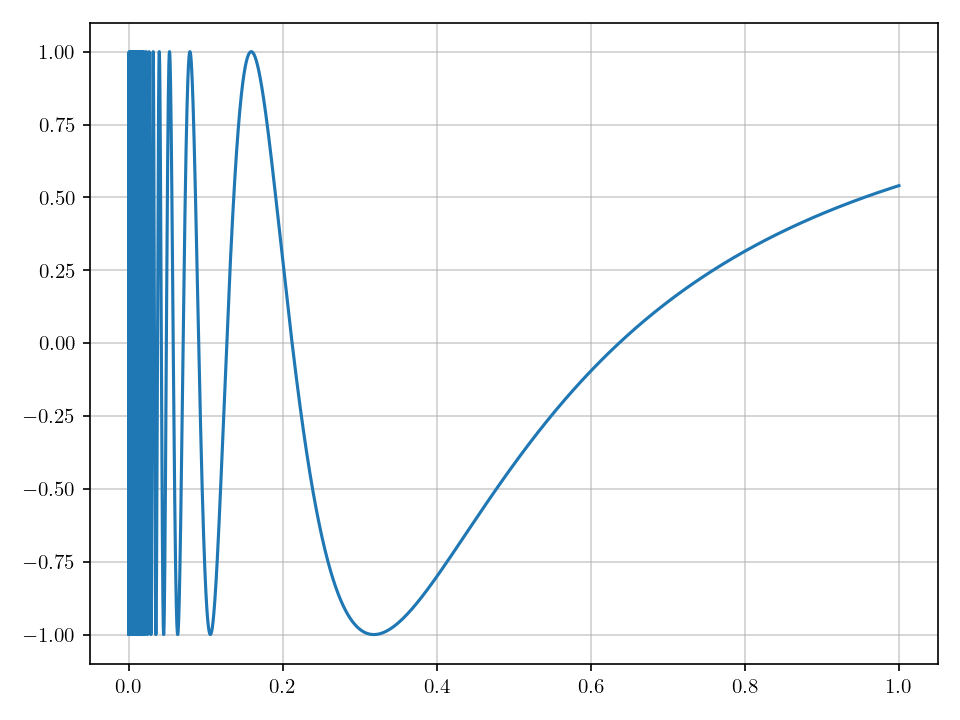
Fig. 2.1 Graph of the function \(f(x) = \cos\frac{1}{x}\) for \(x \in (0, 1]\) and \(f(0) = 0\). It is bounded on \([0, 1]\) but not of bounded variation for it varies rapidly near \(x=0\).

Clearly, this function is bounded by \(1\). But intuitively, it is not of bounded variation since it varies rapidly near \(x=0\). Let \(P\) be a partition of \([0, 1]\) where each \(x_k\) is given by

\[\begin{split}x_k = \begin{cases} \frac{1}{(n-k) \pi}, & 1 \leq k \leq n-1 \\ 0, & k = 0 \\ 1, & k = n \end{cases}\end{split}\]

For \(k=1, \dots, n-1\), we have

\[f(x_k) = \cos( (n-k) \pi) \in\{-1, 1\}\]

The function value is either \(1\) or \(-1\) and the sign alternates between each two consecutive points. Hence,

\[\sum_{k=1}^{n}\abs{\Delta f_k}\geq\sum_{k=2}^{n-1}\abs{\Delta f_k} = 2 (n - 2) \]

As we increase the number of points in the partition, \(\sum \abs{\Delta f_k}\) will exceeds any given number. Therefore, \(f\) is not of bounded variation on \([0, 1]\).

Proposition 2.2

If \(f\) is monotonic on \([a, b]\), then \(f\) is of bounded variation on \([a, b]\).

Proof. Assume \(f\) is increasing. For any partition \(P = \{x_0, \dots, x_n\}\) of \([a, b]\), we have

\[\sum_{k=1}^n \abs{\Delta f_k} = \sum_{k=1}^n (f(x_k) - f(x_{k-1})) = f(b) - f(a) \]

Therefore, \(f\) is of bounded variation on \([a, b]\).

If \(f\) is decreasing, then \(-f\) is increasing. Applying what we have proved, we may conclude that \(-f\) is of bounded variation. Hence, \(f\) is also of bounded variation since \(\sum \abs{\Delta (-f)_k} = \sum \abs{\Delta f_k}\).

Proposition 2.3

Suppose that \(f\) is continuous on \([a, b]\) and the derivative \(f^\prime\) exists in \((a, b)\). If \(\abs{f^\prime(x)} \leq A\) for all \(x \in (a, b)\), then \(f\) is of bounded variation on \([a, b]\).

Note

The assumption that \(f\) being continuous on \([a, b]\), and \(f^\prime\) exists in \((a, b)\) coincides with the mean value theorem. And indeed, it is the key of this proof.

Proof. Let \(P = \{x_0, \dots, x_n\}\) be a partition of \([a, b]\). By the mean value theorem, there exists \(t_k \in (x_{k-1}, x_k)\) for all \(k=1, \dots, n\) such that

\[f(x_k) - f(x_{k-1}) = f^\prime(t_k) (x_k - x_{k-1}) \]

It then follows that

\[\begin{split}\sum_{k=1}^n \abs{\Delta f_k}& = \sum_{k=1}^n \abs{f^\prime(t_k)}(x_k - x_{k-1}) \\& \leq\sum_{k=1}^n A (x_k - x_{k-1}) \\& = A (f(b) - f(a)) \end{split}\]

Therefore, \(f\) is of bounded variation on \([a, b]\).

The following is a well crafted example of showing that a continuous and differentiable function is not necessarily of bounded variation if we do not impose that its derivative is bounded in the interior.

Example 2.2

Consider function defined on \([0, 1]\) given by

\[\begin{split}f(x) = \begin{cases} x \cos \frac{\pi}{2x}, & x \in (0, 1] \\ 0, & x = 0 \end{cases}\end{split}\]

Its graph is shown in Figure Fig. 2.2.

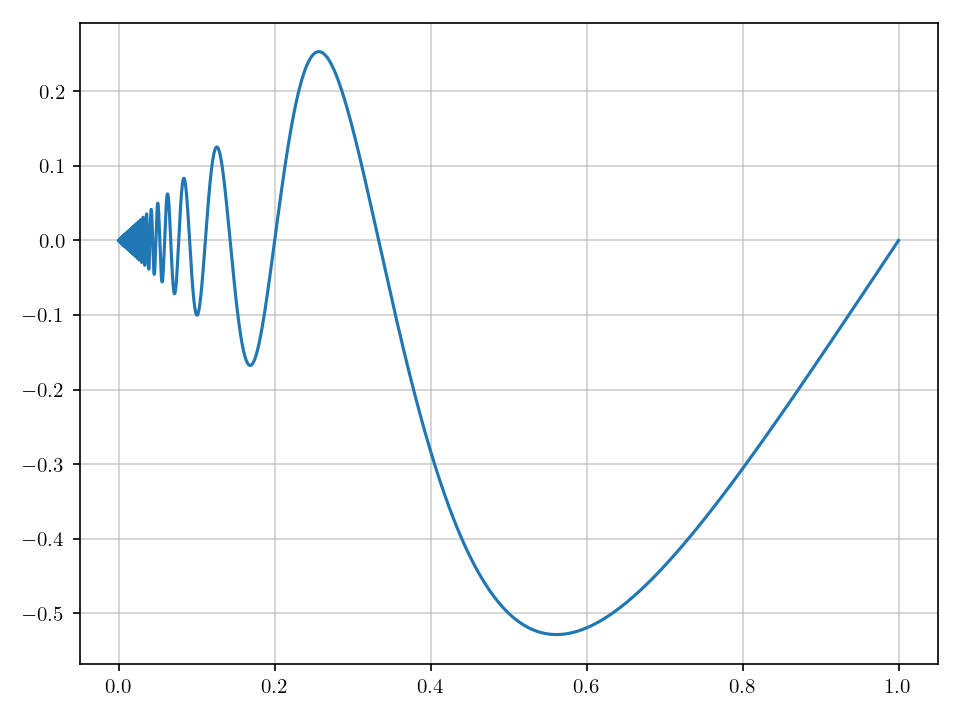
Fig. 2.2 Graph of the function \(f(x) = x \cos \frac{\pi}{2x}\) for \(x \in (0, 1]\) and \(f(0) = 0\). This function is continuous and its derivative exists in \((0, 1)\). But the derivative is unbounded.

The fact that this function is not of bounded variation may be less intuitive than the one given in Example 2.1. The function still varies rapidly near \(x=0\). However, it does not range from \(-1\) and \(1\). Instead, it damps out at \(x=0\) and becomes \(0\). But we will show in the following that we can find a partition so fine that by collecting each small function variation, the overall sum may still increase to infinity.

Consider the partition

\[P = \{0, \frac{1}{2n}, \frac{1}{2n - 1}, \dots, \frac{1}{3}, \frac{1}{2}, 1\}\]

We have

\[\begin{split}\sum_k \abs{\Delta f_k}& = \frac{1}{2n} + \frac{1}{2n} + \frac{1}{2n - 1} + \frac{1}{2n - 1} + \dots + \frac{1}{2} + \frac{1}{2}\\& = 1 + \cdots + \frac{1}{n}\end{split}\]

As \(n\) gets larger and larger, the sum on the right hand-side will increase infinitely for we know that the harmonic series \(\sum \frac{1}{n}\) diverges. Therefore, this function is not of bounded variation.

Of course, the condition of the derivative being bounded is not necessary for a function to be of bounded variation.

Example 2.3

The derivative of the square root function \(f(x) = \sqrt{x}\) in \((0, 1)\) is \(f^\prime(x) = \frac{1}{2\sqrt{x}}\), which tends to infinity as \(x \to 0\). But \(f\) is clearly of bounded variation on \([0, 1]\) by Proposition 2.2 for it is increasing.

Let \(P\) be a partition of \([a, b]\). If we make it finer by adding some intermediate points, then the sum of variations will increase. This result may be helpful in some proofs.

Proposition 2.4

Let \(f\) be defined on \([a, b]\), and \(P\) a partition of \([a, b]\). If \(P^\prime\) is finer than \(P\), i.e., \(P^\prime \supset P\), then

\[v(P^\prime, f) \geq v(P, f) \]

Note

Compare this to the upper and lower Darboux sums when we introduce them in a later section.

Proof. It suffices to that prove for the case where \(P^\prime\) is one point finer than \(P\). Suppose \(P = \{x_0, \dots, x_n\}\) and \(P^\prime = P \sqcup \{c\}\). We have

\[\begin{split}v(P^\prime, f) & = \abs{f(x_1) - f(x_0)} + \cdots + \abs{f(c) - f(x_{j-1})} + \abs{f(x_j) - f(c)} + \cdots + \abs{f(x_n) - f(x_{n-1})}\\& \geq\abs{f(x_1) - f(x_0)} + \cdots + \abs{f(x_j) - f(x_{j-1})} + \cdots + \abs{f(x_n) - f(x_{n-1})}\\& = v(P, f) \end{split}\]

Note

Note that \(j\) may equal to \(1\) or \(n\) in the above notations. We write down the summation in the expanded form to make the proof easier to read.

This completes the proof.