3.8. Euler’s Summation Formula

Euler’s summation formula compares a sum \(\sum f(n)\) with its associated integral \(\int f(x) \dif x\). See Fig. 3.2 for an illustration.

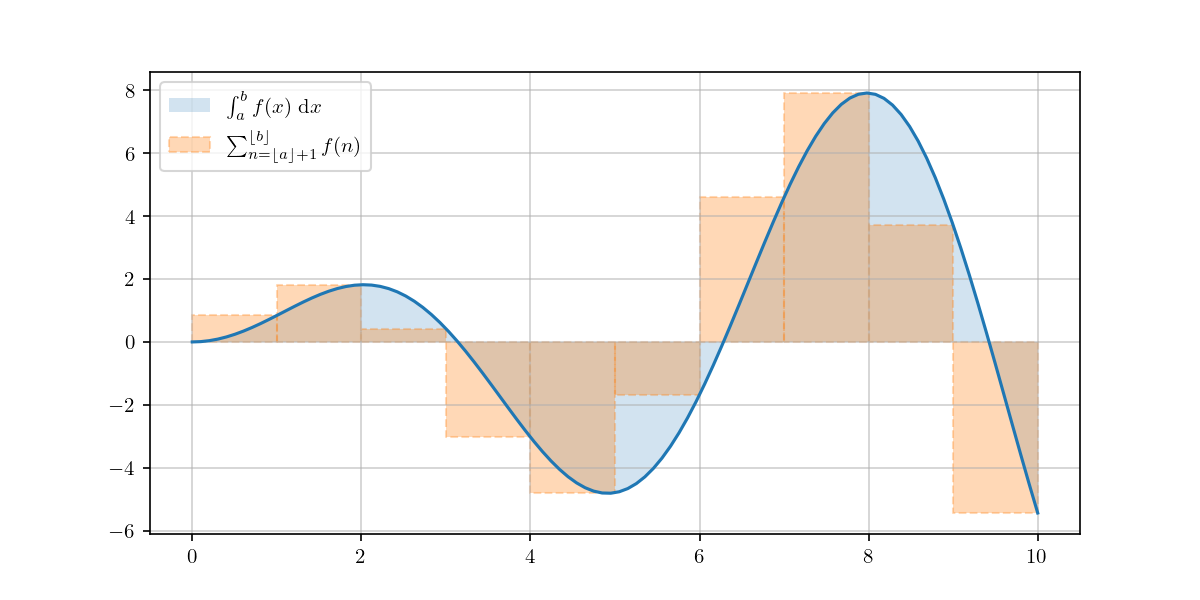
Fig. 3.2 Euler’s Summation Formula.

Theorem 3.10 (Euler’s Summation Formula)

If \(f\) has a continuous derivative \(f^\prime\) on \([a, b]\), then we have

(3.16)\[\sum_{n=\floor{a}+1}^{\floor{b}} f(n) = \int_a^b f(x) \dif x + \int_a^b f^\prime(x) \{x\}\dif x + f(a) \{a\} - f(b) \{b\}\]

In particular, if \(a, b \in \Z\) we have

(3.17)\[\sum_{n=a+1}^{b} f(n) = \int_a^b f(x) \dif x + \int_a^b f^\prime(x) \{x\}\dif x\]

By adding the term \(f(a)\) on both sides and applying the fundamental theorem of calculus, one may obtain a more symmetric formula:

(3.18)\[\sum_{n=a}^b f(n) = \int_a^b f(x) \dif x + \int_a^b f^\prime(x) \left(\{x\} - \frac{1}{2}\right)\dif x + \frac{f(a) + f(b)}{2}\]

Note

(3.17) is easier to use in practice while (3.18) is more elegant in the sense of symmetry. To derive (3.18), we need to use the fundamental theorem of calculus, which will be introduced later.

Proof. Consider a partition of \([\floor{a}+1, \floor{b}]\):

\[P = \{\floor{a}+1, \floor{a}+2, \ldots, \floor{b}\}\]

Applying Theorem 3.8, we have

(3.19)\[\int_{\floor{a}+1}^{\floor{b}} f(x) \dif\floor{x} = \sum_{n=\floor{a}+2}^b f(n)\]

Note

Note that \(n\) starts at \(\floor{a}+2\) since the jump of the floor function \(\floor{x}\) at \(x=\floor{a}+1\) is \(0\).

Next, we examine the integrals \(\int_a^{\floor{a}+1} f(x) \dif \floor{x}\) and \(\int_{\floor{b}}^b f(x) \dif \floor{x}\). It is clear that

(3.20)\[\int_{\floor{b}}^b f(x) \dif\floor{x} = 0\]

because it is zero be definition if \(b \in \Z\) and when \(b \neq \Z\), \(\floor{x} = \floor{b}\) is constant on \([\floor{b}, b]\). Now, we consider \(\floor{x}\) on \([\floor{a}, \floor{a}+1]\). We have

\[\begin{split}\floor{x} = \begin{cases} \floor{a}, & \floor{a} \leq x < \floor{a}+1 \\ \floor{a}+1, & x=\floor{a}+1 \end{cases}\end{split}\]

Therefore, \(\floor{x}\) has a jump \(1\) at \(x=\floor{a}+1\). It then follows that

(3.21)\[\int_a^{\floor{a}+1} f(x) \dif\floor{x} = f(\floor{a}+1)\]

Combining (3.19), (3.20) and (3.21), we obtain

(3.22)\[\int_a^b f(x) \dif\floor{x} = \sum_{n=\floor{a}+1}^b f(n)\]

This expresses the summation in (3.16) as an integral.

The rest of the proof leverages the theorems of integration by parts and reduction of Riemann integrals. Applying integration by parts, we have

(3.23)\[\int_a^b f(x) \dif x + \int_a^b x \dif f(x) = f(b)b - f(a)a\]

and

(3.24)\[\int_a^b f(x) \dif\floor{x} + \int_a^b \floor{x}\dif f(x) = f(b) \floor{b} - f(a) \floor{a}\]

Subtracting (3.24) from (3.23) yields

\[\int_a^b f(x) \dif x - \int_a^b f(x) \dif\floor{x} + \int_a^b \{x\}\dif f(x) = f(b) \{b\} - f(a) \{a\}\]

Since \(f\) has a continuous derivative, by Theorem 3.6, we can replace \(\dif f(x)\) with \(f^\prime(x) \dif x\). Then rearranging the terms, we obtain

(3.25)\[\int_a^b f(x) \dif\floor{x} = \int_a^b f(x)\dif x + \int_a^b f^\prime(x) \{x\}\dif x + f(a) \{a\} - f(b) \{b\}\]

(3.16) is proved by comparing (3.22) and (3.25).

Example 3.1

Using the Euler’s summation formula (3.17), we can derive the following identities related to summing up terms of the form \(\frac{1}{k^s}\):

1. If \(s \neq 1\)

\[ \begin{align}\begin{aligned}\sum_{k=1}^n \frac{1}{k^s} = \frac{1}{n^{s-1}} + s \int_1^n \frac{\floor{x}}{x^{s+1}}\dif x\\```2. If $s=1$ ```{math} :label: eq:39 \sum_{k=1}^n \frac{1}{k} = \ln n - \int_1^n \frac{\{x\}}{x^{2}}\dif x + 1\\```{eq}`eq:39` provides another way of proving the sequence $\left\{ \sum_{1}^n \frac{1}{k} - \ln n\right\}$ converges (to Euler's constant $\gamma$). And hence, we obtain an integral form of the Euler's constant:\\```{math} \gamma = 1 - \int_1^\infty\ \frac{\{x\}}{x^2}\dif x \end{aligned}\end{align} \]