2.1. Definition of Trees

A tree is a connected acyclic graph. A tree is clearly a simple graph for there cannot be any loops (1-cycles) or parallel edges (2-cycles).

If a tree \(T\) is nontrivial, then the degree of every vertex must greater than or equal to 1 since a tree is connected. Moreover, there always exists at least one vertex with degree 1, that is,

\[\begin{align*}\delta(T) = 1 \end{align*}\]

If this is not the case, then we end up with a graph with

\(\delta \geq 2\). But this further implies that there exists a cycle in the graph by Proposition 1.9, contradicting the definition of a tree.

If the reader has a background of computer science, then the tree data structure one might be familiar with is actually what we call a rooted tree with one vertex called the root with special treatment. However, the tree we defined here is an unrooted tree, or free tree, since we often do not specify the root vertex.

A tree leaf is a vertex of degree 1. Note that it is possible that the degree of the tree root is 1 if it is specified. But we often do not call it a leaf. Hence, in a rooted tree, a leaf is a non-root vertex of degree 1. Clearly, a nontrivial tree always has a leaf. In fact, it always has at least two leafs, as we shall see in Corollary 2.1.

Theorem 2.1

In a tree \(T\), any two distinct vertices are connected by a unique path.

Proof. Assume there are two distinct \((u,v)\)-paths, \(P_1\) and \(P_2\)(regraded as path graphs). Then there exists at least one distinct edge in these two, say \(e=xy\). Without loss of generality, we may assume \(e \in V(P_1)\).

Consider the graph \(P_1 \cup P_2 - e\). We claim that it contains a \((x,y)\)-path. To see this, we note that there exist a \((x,u)\)-path and a \((v,y)\)-path in \(P_1\), and also a \((u,v)\)-path in \(P_2\). By concatenating all these three paths, we will obtain a \((x,y)\)-walk (not necessarily a path). But by Proposition 1.8, we can always extract a \((x,y)\)-path from it, say \(P_3\).

Now, we have two distinct paths from \(x\) to \(y\) in \(T\). One is \(xy\) and the other is \(P_3\), which contradicts the hypothesis.

The graph in Fig. 2.1 is certainly not a tree. But any two distinct vertices are indeed connected by a unique path. Therefore, for the converse of Theorem 2.1 to hold, we need to exclude the cases where graphs contain loops.

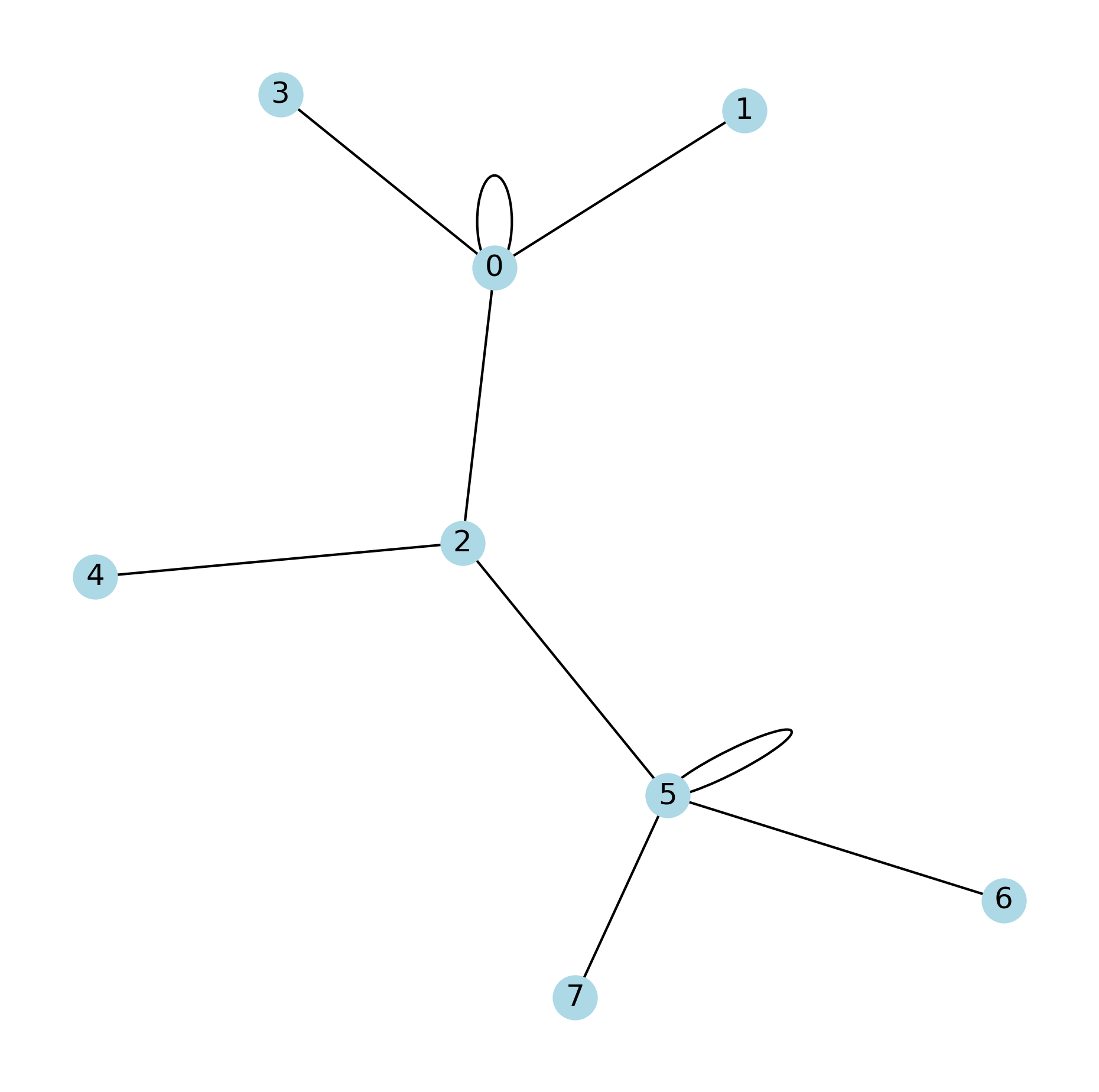
Fig. 2.1 It will become a tree if the loops are removed.

Theorem 2.2

If graph \(T\) is loopless and there exists one and only one path connecting each pair of distinct vertices, then \(T\) is a tree.

Proof. First, note that \(T\) is connected. Assume, on the contrary, there exists a cycle \(C\) in \(G\). Let \(e\) be an edge in \(C\). Since \(T\) is assumed loopless, the two ends of \(e\) must be distinct, say \(x\) and \(y\).

Note that there exists a \((x,y)\)-path in \(C - e\), which is different from the path \(xy\). (In fact, this path is \(C-e\) itself.) This leads to a contradiction.

Theorem 2.3

Let \(T\) be a tree. Then we have

(2.1)\[\begin{align}\abs{E} = \abs{V} - 1 \end{align}\]

Proof. We shall prove by induction on the order \(\abs{V}\).

Base Case: If \(\abs{V} = 1\), then \(T\) is a trivial graph without any edges, and hence (2.1) holds.

Inductive Step: Assume this theorem holds for any trees with order \(k\). Suppose now \(\abs{V(T)} = k+1\). Pick a leaf \(v\), and then remove it from \(T\). This is always possible as we have noted. Observe that \(T - v\) remains a tree. And by removing \(v\), we only remove a single edge from \(T\) since \(\deg(v) = 1\). Therefore, \(\abs{E(T-v)} = \abs{E(T)} - 1\). But by the induction hypothesis, we know \(\abs{E(T-v)} = \abs{V(T-v)} - 1 = k - 1\). It then follows that

\[\begin{align*}\abs{E(T)} = \abs{E(T-v)} + 1 = k-1+1 = (k+1)-1 = \abs{V(T)} - 1 \end{align*}\]

This completes the proof.

Corollary 2.1

Every nontrivial tree has at least two leafs.

Proof. As we have noted, a nontrivial tree \(T\) has at least one leaf. Assume \(T\) only has one leaf. Then we have

\[\begin{align*}\sum_{v \in V}\deg(v) \geq 1 + 2 (\abs{V} - 1) = 2 \abs{V} - 1 \end{align*}\]

since all vertices, except one, are of degree at least 2. Combined with Theorem 1.1, we know

(2.2)\[\begin{align} 2\abs{E} = \sum_{v \in V}\deg(v) = 2 \abs{V} - 1 \end{align}\]

On the other hand, it follows from Theorem 2.3 that

(2.3)\[\begin{align} 2\abs{E} = 2 \abs{V} - 2 \end{align}\]

Note that equations (2.2) and (2.3) contradict each other. Therefore, \(T\) has at least two leafs.

Theorem 2.4

Let \(T\) be a graph with \(\abs{T}-1\) edges, then the following statements are equivalent:

• ➀ \(T\) is a tree.

• ➁ \(T\) is connected.

• ➂ \(T\) is acyclic.

Proof. Note that we only need to show 2 \(\implies\) 3 and 3 \(\implies\) 2.

(2 \(\implies\) 3) By Proposition 1.7, we know \(T\) is a connected graph with minimum number of edges. We need to show \(T\) is acyclic. Assume that, on the contrary, there exists a cycle \(C\) in \(T\). Pick an edge \(e\) in \(C\). Note that \(e\) cannot be a cut edge by Theorem 1.4. Therefore, \(G-e\) remains connected. But clearly \(G-e\) has one less edge than that of \(G\), which leads to a contradiction. Therefore, \(T\) is indeed acyclic.

(3 \(\implies\) 2) This direction follows directly from Proposition 1.11.