1.4. Paths and Connection

A walk in a graph is a sequence of edges \(e_1 \cdots e_k\) joining a nonempty sequence of vertices \(v_0 v_1 \cdots v_k\), which is denoted by

(1.3)\[\begin{align} v_0 e_1 v_1 \cdots e_k v_k \end{align}\]

with each edge written after one of its end and followed by its other end. Note that though the sequence of vertices in a walk is required to be nonempty, the sequence of edges may be empty. And in that case, the walk contains only one vertex, say \(v_0\), and it is called the trivial walk.

Note

The term sequence in mathematics often means an infinite sequence, which is essentially a function defined on \(\N^\ast\). However, in graph theory, we usually refer to sequence as a finite list of ordered elements.

We call a walk \(W\) from \(v_0\) to \(v_k\) a \((v_0, v_k)\)-walk. The vertices \(v_0\) and \(v_k\) are referred to as the origin and the terminus of that walk, respectively.

It should be emphasized that neither the edges nor the vertices in a walk are necessarily distinct. However, if all edges of walk \(W\) are distinct, we call \(W\) a trail. And if all vertices in \(W\) are distinct, it is then called a path. Of course, all edges in a path are also distinct since the vertices are.

Two vertices are said to be connected if there exists a path joining them. Otherwise, they are disconnected.

The length of a path \(P\), written as \(\abs{P}\), is defined as the number of edges along it. Note that the length of a trivial path is zero since there are no edges.

If \(G\) is a simple graph, then we may write a walk simply as a sequence of vertices since there is one and only one edge joining each pair of consecutive vertices in the walk. For example, we write the \((v_0, v_k)\)-walk in (1.3) as

\[\begin{align*} v_0 v_1 \cdots v_k \end{align*}\]

with edges dropped.

Proposition 1.8

If there is a \((u, v)\)-walk in \(G\), then there is also a \((u, v)\)-path in \(G\).

This can be proved easily using the following algorithm (Algorithm 1.2).

Algorithm 1.2 (Extracting a Path From a Walk)

Proposition 1.5

The number \((v_i, v_j)\)-walks of length \(k\) in \(G\) is the \((i,j)\)-th entry of the \(k\)-th power of the adjacency matrix \(A\), i.e., \(A^k\).

Proof. TODO

Imagine removing one edge from the original graph \(G\). Then we can obtain at most one more component by cutting in half one of \(G\)’s components. See Fig. 1.3.

To prove this, we first consider the following useful lemma.

Lemma 1.2

Let \(G\) be a connected graph, and \(e\) be one of its edges. Suppose that the two ends of \(e\) are \(x\) and \(y\). Then every vertex \(v\) is either connected to \(x\) or \(y\) in \(G-e\).

Proof. First, suppose that \(e\) is a loop. Since \(G\) is connected, every two vertices are connected by a path. And they remain connected in \(G-e\) since a path cannot contain any loops. Hence, in this case, every vertex \(v\) is connected to both \(x\) and \(y\) in \(G-e\).

Assume \(e\) is not a loop. If vertex \(v\) is no longer connected to \(x\) in \(G-e\), then \(v\) must be originally connected to \(x\) in \(G\) by a path \(P\) containing the edge \(e\). Note that \(P\) is of the form

\[\begin{align*} P = v \cdots y e x \end{align*}\]

Because the \((v,y)\)-section of \(P\) does not traverse \(e\), \(v\) is connected to \(y\) in \(G-e\) by this \((v,y)\)-section. Hence, we have shown that, in subgraph \(G-e\), \(v\) must be connected to \(y\) if it is disconnected from \(x\). This completes the proof.

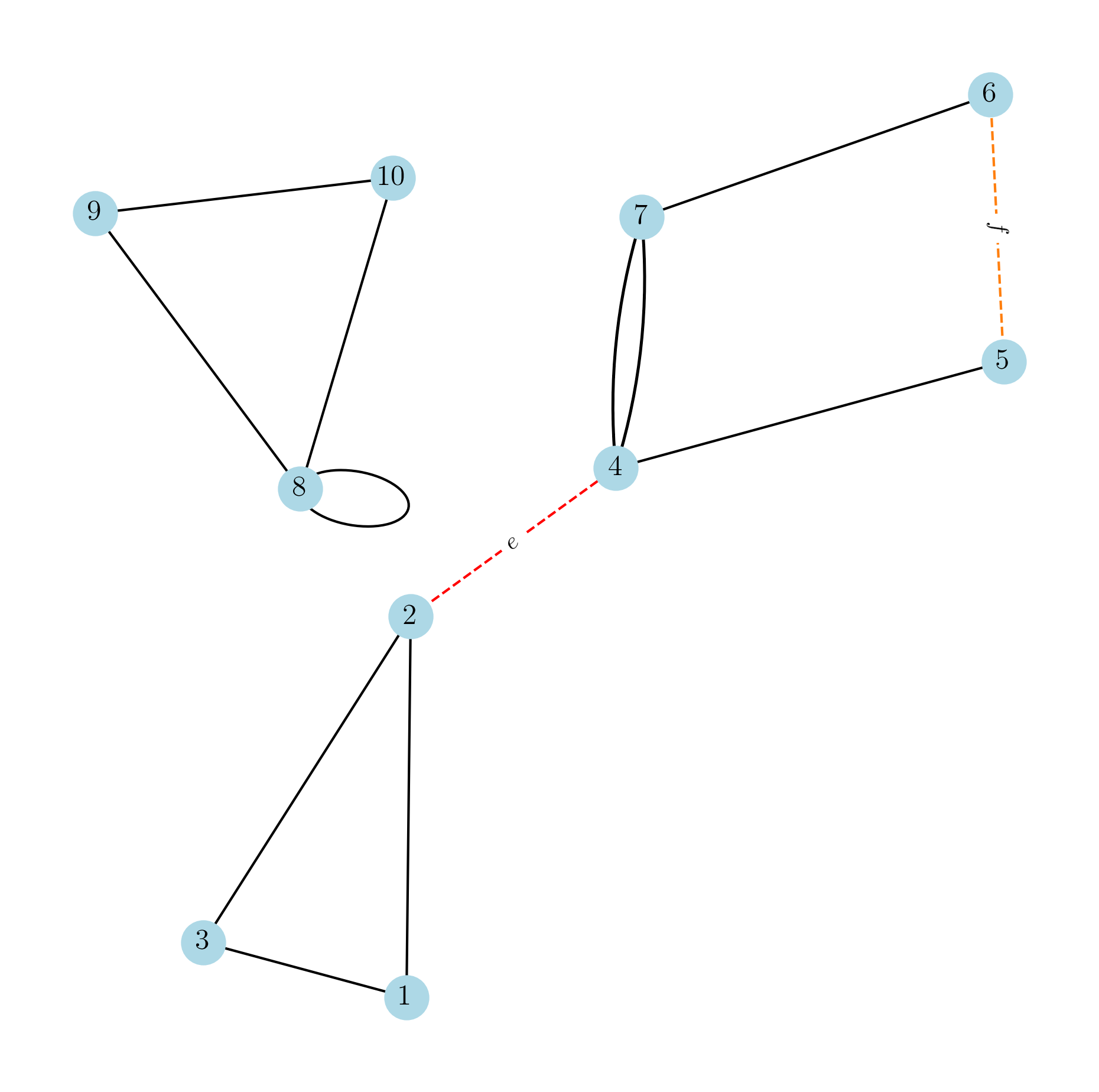
Fig. 1.3 The graph \(G\) has 2 components. If we remove edge \(f\), then \(G-f\) still has 2 components. But if we remove edge \(e\), then the remaining graph \(G-e\) has 3 components.

Proposition 1.6

If \(e \in E\), then we have

(1.4)\[\begin{align}\omega(G) \leq\omega(G-e) \leq\omega(G) + 1 \end{align}\]

Inequalities (1.4) describe the result of cutting an edge in a compact way. The first inequality \(\omega(G) \leq \omega(G-e)\) says the number of components may increase by cutting an edge. While the second inequality says this number will be increased by at most one.

Proof. If \(e\) is a loop, then the conclusion is trivial. We assume \(e = xy\) is not a loop, i.e., \(x\) and \(y\) are distinct, in the rest of the proof. Suppose that the components of \(G\) are \(G[V_1], \ldots, G[V_\omega]\). Without loss of generality, we may also assume that \(x, y \in V_1\).

(Case 1) Suppose that there exists a \((x,y)\)-path in \(G-e\), then \(x\) is still connected to \(y\) in \(G-e\), i.e., \(x \sim y\) in \(G-e\). Pick an arbitrary vertex \(v \in V_1\). By Lemma 1.2, we know either \(v \sim x\) or \(v \sim y\). Either way, by the transitivity, we have \(v \sim x\) since \(x \sim y\). Therefore,

\[\begin{align*} v \sim x \quad\forall v \in V_1 \end{align*}\]

This means \(V_1\) remains a equivalent class in \(G-e\). In this case, \(\omega(G-e) = \omega(G)\).

(Case 2) We now consider the case where \(x\) is disconnected from \(y\) in \(G-e\). For any vertex \(v \in V_1\), by Lemma 1.2, we have either \(v \sim x\) or \(v \sim y\). But \(v\) cannot be connected to both \(x\) and \(y\) since \(x\) and \(y\) are assumed disconnected from each other. It then follows that \(V_1\) can be partitioned into two equivalent classes, \([x]\) and \([y]\). In other words, \(V_1\) is split into two components in \(G-e\). Therefore, \(G-e\) has one more component than that of \(G\), and hence \(\omega(G-e) = \omega(G) + 1\).

The idea of cutting an edge is quite helpful in many proofs since by doing so, we will probably divide the original graph into two smaller ones.

The edge if removed will indeed results in one more component deserves a name, as we shall define in the following.

Definition 1.2

The edge \(e\) of \(G\) is called a cut edge if

(1.5)\[\begin{align}\omega(G-e) = \omega(G) + 1 \end{align}\]

In Fig. 1.3, \(e\) is a cut edge of \(G\) but \(f\) is not.

Note

Equation (1.5) is replaced by \(\omega(G-e) > \omega(G)\) in [Bondy and Murty, 1976]. But since we have already proved Proposition 1.6, we can be more specific.

Consider a path graph \(P_n\) on \(n\) vertices. It is connected and it has altogether \(n-1\) edges. Apparently, if we remove any edge from it, then we will end up with a disconnected graph. This somehow tells us that for a graph to be connected, it cannot have too few edges, which leads to the question that what is the minimum number of edges of a connected graph of order \(n\)?

Proposition 1.7

The minimum number of edges of a connected graph on \(n\) vertices is \(n-1\).

Proof. We shall prove by induction on the order. The induction hypothesis is that if \(G\) is a connected graph \(G\) with minimum number of edges and its order is less than or equal to \(n\), then it has exactly \(n-1\) edges.

Base Case: If \(G\) is a trivial graph, then clearly it has no edges.

Inductive Step: Assume the hypothesis holds for \(n = k\). Note that we only need to show \(G\) has \(k\) edges under the case where \(G\) is of order \(k+1\). Because \(G\) is a connected graph with minimum number of edges. By removing any edge, say \(e\), from \(G\) will result in a disconnected graph \(G-e\). And by Proposition 1.6, we know \(G-e\) has two components, say \(G_1\) and \(G_2\). Note that both \(G_1\) and \(G_2\) are of orders less than or equal to \(k\), say \(n_1\) and \(n_2\), respectively. Moreover, both \(G_1\) and \(G_2\) are connected graphs with minimum number of edges. Hence, applying the induction hypothesis to both \(G_1\) and \(G_2\), we conclude that

\[\begin{align*}\abs{E(G_1)} = n_1 - 1 \quad\text{and}\quad\abs{E(G_2)} = n_2 - 1 \end{align*}\]

Therefore, the total number of edges of \(G\) is

\[\begin{align*}\abs{E(G)} = \abs{E(G_1)} + \abs{E(G_2)} + 1 = n_1 - 1 + n_2 - 1 + 1 = n_1 + n_2 - 1 = \abs{V(G)} - 1 = k \end{align*}\]

The second last equality follows from the fact that the vertices of \(G\) is partitioned into vertices of \(G_1\) and \(G_2\), respectively, since \(G_1\) and \(G_2\) are complements. This completes the proof.

Apart from the path graph \(P_n\), Fig. 1.4 also depicts several other connected graphs of order 6 with minimum number of edges, in this case, 5 edges. Such graphs are called trees, as we will formally introduce in Trees.

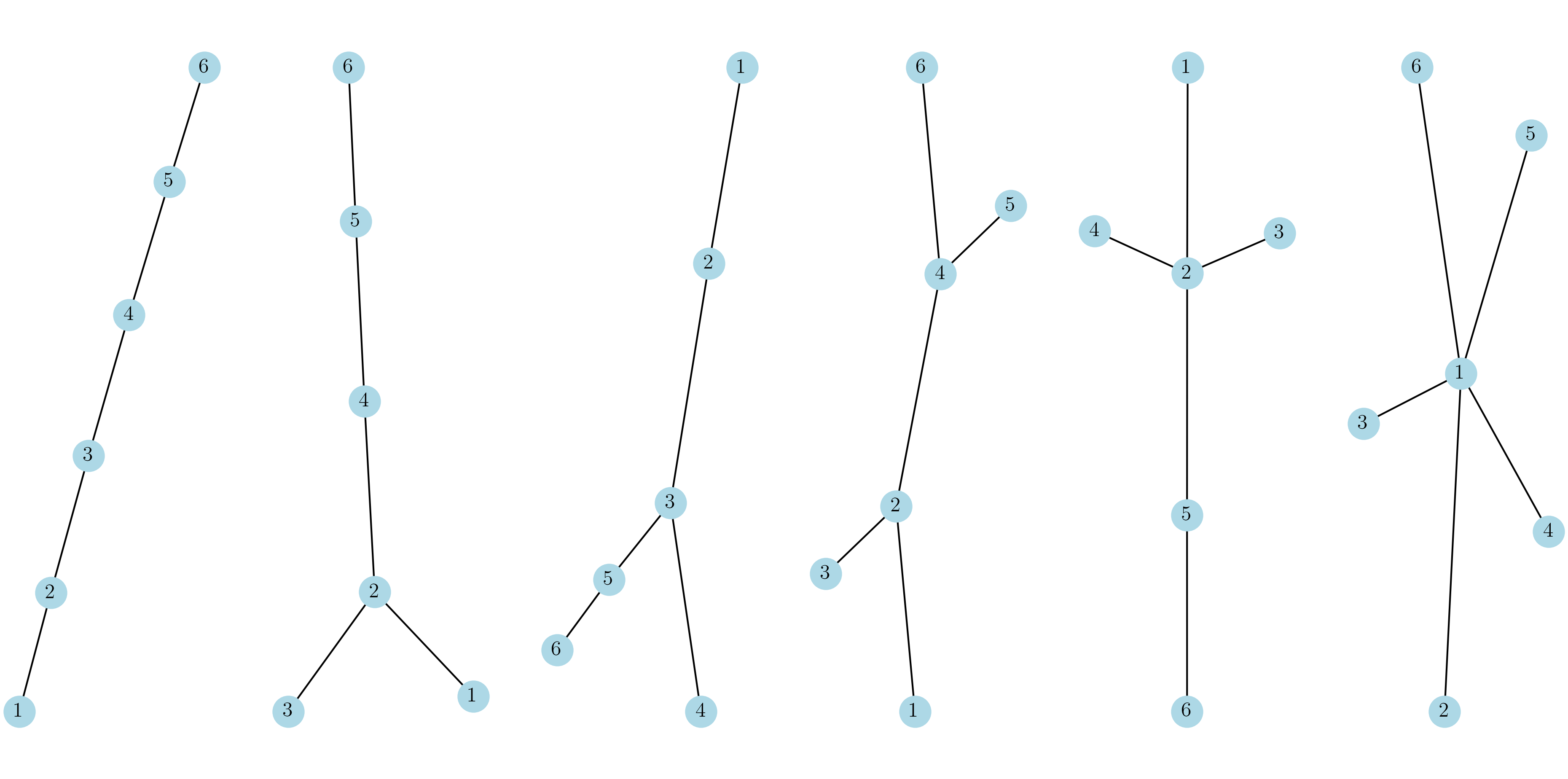
Fig. 1.4 Connected graphs on 6 vertices with minimum number of edges, i.e., 5 edges.

Proposition 1.8

Let \(G\) be a simple and connected graph with order greater than or equal to 3. If \(G\) is not complete, then there exist three vertices \(u\), \(v\) and \(w\) such that \(uv, vw \in E\) but \(uw \notin E\).

Proof. Because \(G\) is not complete, there exist two vertices \(u\) and \(w\) that are not incident. Let \(P\) be a shortest path from \(u\) to \(w\).

If \(P\) is of length 2, then we can write \(P = u v w\). Edges \(uv\) and \(vw\) exist in \(G\). But the edge \(uw\) does not, which is as desired.

If the length of \(P\) is greater than or equal to \(3\), then \(P\) is of the form

\[\begin{align*} P = u x v \cdots w \end{align*}\]

Note that \(uv \notin E\). Otherwise, \(u v \cdots w\) would be a shorter \((u,w)\)-path than \(P\). In this case the vertices \(u\), \(x\) and \(v\) are as desired.