1.5. Cycles

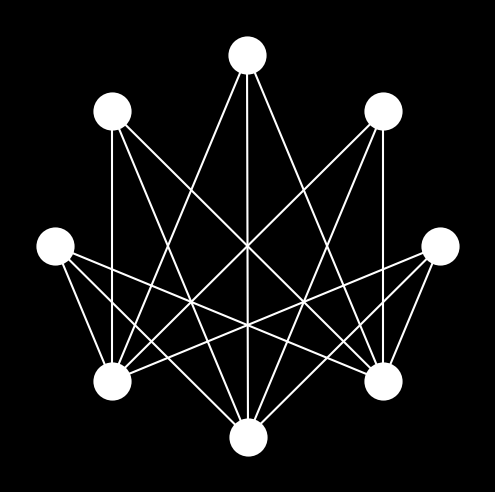
One simple yet useful observation of a particular longest path in a graph is that all the neighbors of the terminus must occur along the path. To be specific, if \(P = v_0 e_1 v_1 \cdots e_k v_k\) is one of the longest paths in \(G\) then \(P\) must contain all vertices in \(N(v_k)\). To prove this, we assume \(P\) does not contain \(v_{k+1} \in N(v_k)\). (Suppose \(\psi(e_{k+1}) = v_k v_{k+1}\).) Then the path \(P + e_{k+1}v_{k+1}\) is clearly longer than \(P\), which leads to a contradiction. Fig. 1.5 depicts such an example. Note that if \(8\) were a neighbor of \(7\), then path \(12345678\) would be longer.

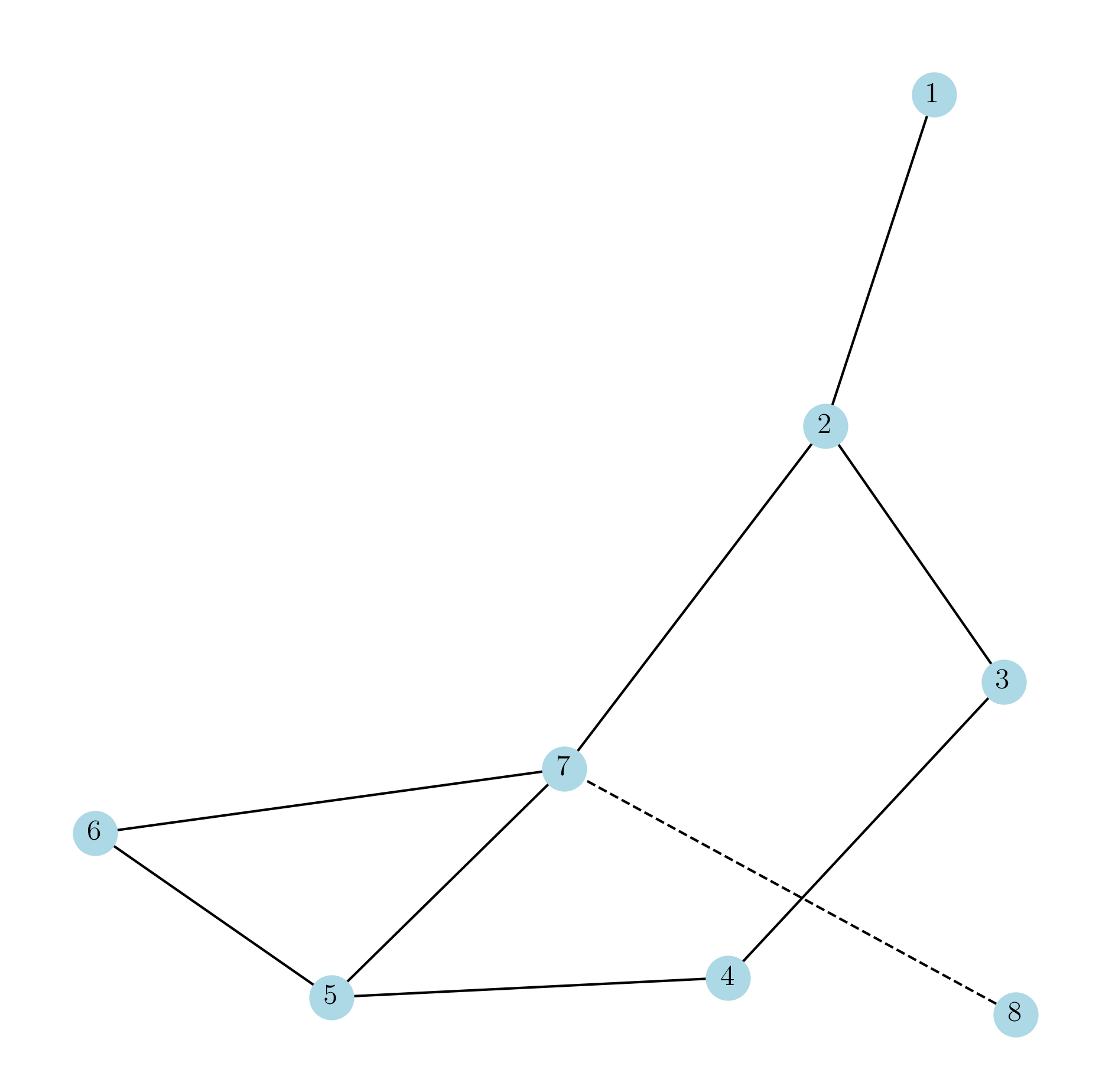
Fig. 1.5 Path \(1234567\) is one of the longest paths.

Proposition 1.9

If \(G\) is a simple graph with \(\delta(G) \geq 2\), then there exists a cycle of length at least \(\delta(G)+1\).

Proof. Let \(P = u \cdots v\) be a longest path in \(G\). As noted before, all the neighbors of the terminus \( v \), denoted by \(v_1, \ldots, v_{\delta(G)}\) arranged by their original order in \(P\), must occur along the path \(P\). Note that the \((v_1, v)\)-section, denoted by \(Q\), is of length \(\delta(G)\). Because \(\deg(v) \geq 2\), \(v\) has at least two neighbors. In other words, the section \(Q\) is different from the edge connecting \(v\) and \(v_1\). Hence, \(Q v_1\) forms a cycle. And it is of length \(\delta(G) + 1\). This completes the proof.

In fact, we have an algorithm to find a cycle without knowing the longest path in \(G\).

Algorithm 1.3 (Finding a Cycle in \(G\) With \(\delta(G) \geq 2\))

Proof. We need to show that Algorithm 1.3 works correctly.

Initialization: Firstly, note that line 7 is possible since \(v_0\) has no loops and \(\deg(v_0) \geq 2\).

We claim the loop invariants are

• ➀ \(P\) has \(j\) vertices assuming that we are to execute the \(j\)-th iteration,

• ➁ \(P\) has no duplicated vertices, i.e., \(P\) is a path, and

• ➂ edge \(e\) is incident with \(v\).

Maintenance: Suppose we are in the \(j\)-th iteration. After line 9, \(P\) remains a path. Because \(\deg(v) \geq 2\), there exists an edge \(f\) other than \(e\) that is incident with \(v\). Hence, line 10 works correctly. After executing line 12, we find that the number of vertices in \(P\) is increased by one, i.e., \(j+1\), \(P\) is still a path and \(e\) is incident with \(v\).

Termination: We can complete at most \(n-1\) iterations since \(P\) can hold at most as many vertices as there are in \(G\). Upon termination, we find \(v\) is in \(P\) and \(e\) is incident with \(v\). By removing from \(P\) all vertices and edges before \(v\) and then append to it edge \(e\) and vertex \(v\), we will obtain a cycle from \(v\) to itself.

Theorem 1.3

Graph \(G\) is a bipartite graph if and only if it contains no odd cycles.

Proof. TODO

The girth of a graph is defined as the length of its shortest cycle. We say the girth of \(G\) is infinity if it contains no cycles. Apparently, if \(G\) has girth 1, then it contains a loop. If it has girth 2, then there must be a parallel edge. But it has no loops. And if the girth of \(G\) is greater than or equal to 3, then it must be a simple graph.

Proposition 1.10

A \(k\)-regular graph with girth 4 has at least \(2k\) vertices. Moreover, if it has exactly \(2k\) vertices, then it must be \(K_{k,k}\), i.e., a complete bipartite graph with both sides of the bipartition having the same size \(k\). Conversely, \(K_{k,k}\) is a \(k\)-regular graph with girth 4.

Fig. 1.6 depicts several \(K_{k,k}\) graphs.

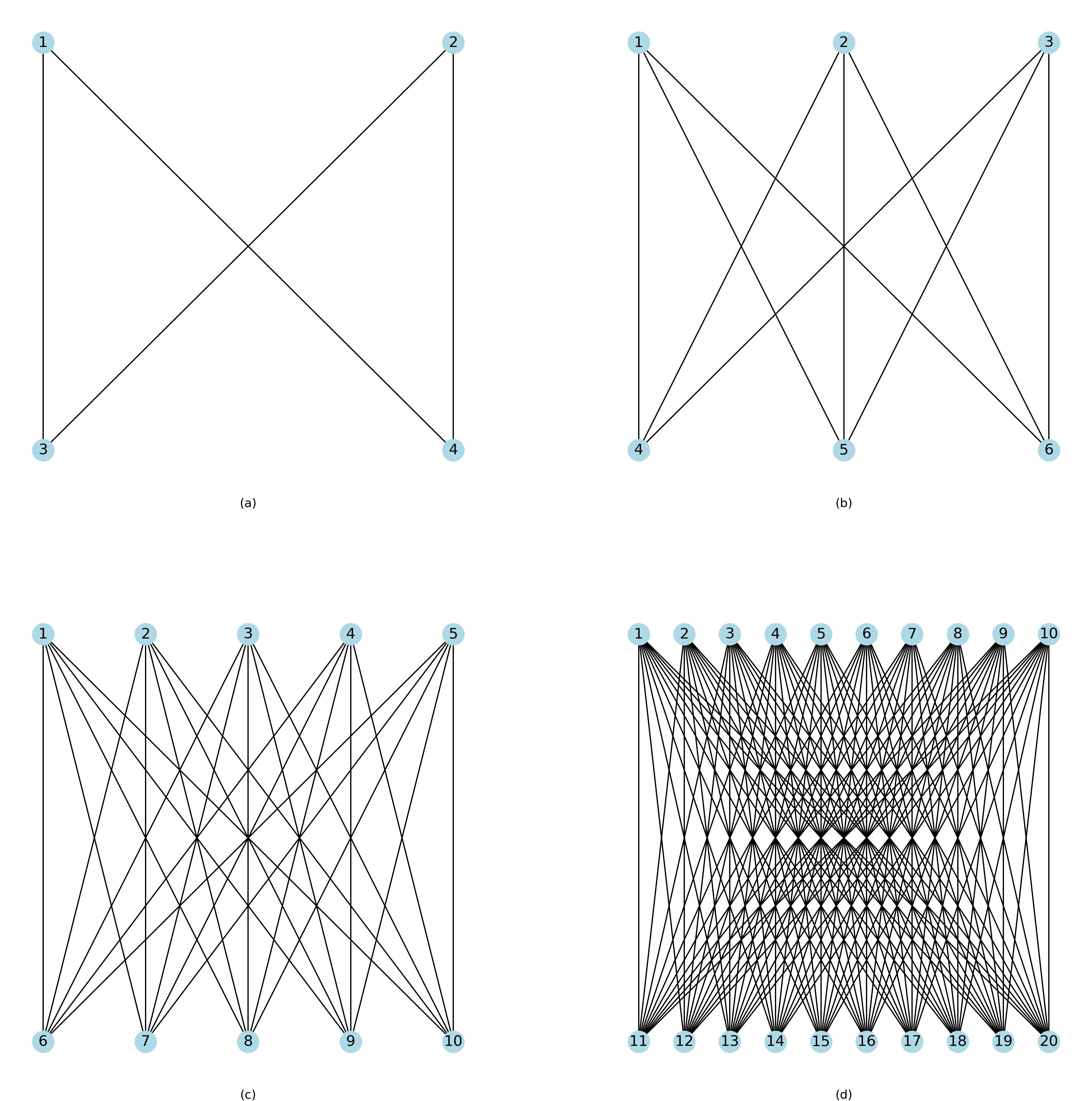
Fig. 1.6 (a) \(K_{2,2}\). (b) \(K_{3,3}\). (c) \(K_{5,5}\). (d) \(K_{10,10}\).

Proof. Take a pair of incident vertices \(u\) and \(v\) in \(G\). We have \(N(u) \cap N(v) = \emptyset\). Otherwise, a triangle would appear. Because the degrees of \(u\) and \(v\) are both \(k\), equivalently, the sizes of their neighbors are \(k\), \(G\) must has at least \(2k\) vertices having these two disjoint sets \(N(u)\) and \(N(v)\).

Suppose \(\abs{V} = 2k\). Pick a pair of incident vertices \(u\) and \(v\) as before. From the previous proof, we know \(\abs{N(u)} = \abs{N(v)} = k\) and they are disjoint. Since \(G\) now only has \(2k\) vertices, \(V\) is composed of these two neighbor sets, i.e., \(V = N(u) \uplus N(v)\). Observe that each pair of vertices in \(N(u)\) cannot be joined with each other for there are no triangles. The same conclusion also holds for \(N(v)\). Therefore, every vertex in \(N(u)\) is joined with every vertex in \(N(v)\) because the degree of every vertex is \(k\). This shows that \(G\) is \(K_{k,k}\).

We also need to show \(K_{k,k}\) is a \(k\)-regular graph with girth 4. Clearly, it is \(k\)-regular. It contains no cycles with length 1 or 3 by Theorem 1.3. Of course, it does have any parallel edges, hence no 2-cycles. And we can easily find a 4-cycle in it. For example, if we suppose \(X=\{x_1,\ldots,x_k\}\) and \(Y=\{y_1,\ldots,y_k\}\) form a bipartition of \(K_{k,k}\), then \(x_1 y_1 x_2 y_2 x_1\) is a 4-cycle.

We call a graph acyclic if it contains no cycles.

The next theorem is useful to determine whether an edge is a cut edge by checking that if it is contained in any cycles.

Theorem 1.4

An edge \(e\) is an cut edge of \(G\) if and only if it is contained in no cycles of \(G\).

Proof. In the following proof, we suppose that the two ends of \(e\) are \(x\) and \(y\) and that they are in the path equivalent class \(V_1\). Then, by Lemma 1.2, we know every vertex \(v\) in \(V_1\) is either connected to \(x\) or \(y\) in subgraph \(G-e\).

(\(\implies\)) We first exclude the case where \(e\) is a loop. For the rest scenarios, we shall prove the contrapositive. Suppose \(e\) is contained in some cycle \(C\). Then \(C-e\) is a path joining \(x\) and \(y\). This implies that \(x\) and \(y\) remain connected in \(G-e\). Therefore, for each \(v \in V_1\), \(v\) is connected to both \(x\) and \(y\) in \(G-e\). In other words, \((G-e)[V_1]\) is connected. Since no additional components will appear in \(G-e\), \(e\) is not an cut edge.

(\(\impliedby\)) If \(e\) is contained in no cycles of \(G\), then \(x\) and \(y\) are disconnected in \(G-e\). Hence, \((G-e)[V_1]\) is then disconnected. Therefore, \(\omega(G-e) > \omega(G)\), which further implies that \(e\) is a cut edge.

As we can imagine, an acyclic graph cannot have too many edges. Interestingly, an acyclic graph with maximum number of edges is exactly a connected graph with minimum number of edges. Compare the following proposition with Proposition 1.7.

Proposition 1.11

The maximum number of edges of an acyclic graph \(G\) on \(n\) vertices is \(n-1\). Furthermore, in this case, \(G\) is also connected.

Proof. Suppose \(G\) is an acyclic graph with maximum number of edges. We are going to show that \(G\) is in fact a connected graph with minimum number of edges.

We first show that \(G\) is connected. Assume \(G\) is not connected. Then there exist two distinct vertices \(u\) and \(v\) such that there are no paths between them. Of course, \(uv \notin E\). By adding the edge \(uv\), \(G + uv\) remains acyclic. But then \(G + uv\) has more edge than that of \(G\), which contradicts the assumption that \(G\) is an acyclic graph with maximum number of edges. Therefore, we see that \(G\) must be connected.

On the other hand, choose an edge \(e\) and we will find that \(e\) is contained in no cycles since \(G\) is acyclic. By Theorem 1.4, \(e\) is a cut edge. Hence, \(G-e\) is disconnected. This implies that \(G\) is a connected graph with minimum number of edges. Therefore, \(G\) has exactly \(n-1\) edges by Proposition 1.7.