LSTM#
Imports#
from typing import Self, Optional
from pprint import pprint
from io import StringIO
from collections import OrderedDict
import numpy as np
import pandas as pd
from sklearn.base import BaseEstimator, TransformerMixin
from sklearn.model_selection import train_test_split
import torch
from torch import sigmoid, tanh
from torch import nn
torch.manual_seed(42)
<torch._C.Generator at 0x14998ee10>
LSTM Cell#
# Input size of x, i.e.,
# number of features of x
d = 3
# Hidden size, i.e.,
# size of the hidden state vector h
# In fact, all vectors involved in an LSTM cell
# other than x share the same size
k = 2
lstm_cell = nn.LSTMCell(
input_size=d,
hidden_size=k,
)
print(f"model parameters: {lstm_cell.state_dict().keys()}")
model parameters: odict_keys(['weight_ih', 'weight_hh', 'bias_ih', 'bias_hh'])
W_ih = lstm_cell.state_dict()["weight_ih"]
bias_ih = lstm_cell.state_dict()["bias_ih"]
W_hh = lstm_cell.state_dict()["weight_hh"]
bias_hh = lstm_cell.state_dict()["bias_hh"]
print("shape:")
print(f"W_ih: {W_ih.shape}\tbias_ih: {bias_ih.shape}")
print(f"W_hh: {W_hh.shape}\tbias_hh: {bias_hh.shape}")
shape:
W_ih: torch.Size([8, 3]) bias_ih: torch.Size([8])
W_hh: torch.Size([8, 2]) bias_hh: torch.Size([8])
W_ii, W_if, W_ig, W_io = torch.split(W_ih, k)
bias_ii, bias_if, bias_ig, bias_io = torch.split(bias_ih, k)
W_hi, W_hf, W_hg, W_ho = torch.split(W_hh, k)
bias_hi, bias_hf, bias_hg, bias_ho = torch.split(bias_hh, k)
print("shapes of weights and biases of the input gate:")
print(f"W_ii: {W_ii.shape}\tbias_ii: {bias_ii.shape}")
print(f"W_hi: {W_hi.shape}\tbias_hi: {bias_hi.shape}")
shapes of weights and biases of the input gate:
W_ii: torch.Size([2, 3]) bias_ii: torch.Size([2])
W_hi: torch.Size([2, 2]) bias_hi: torch.Size([2])
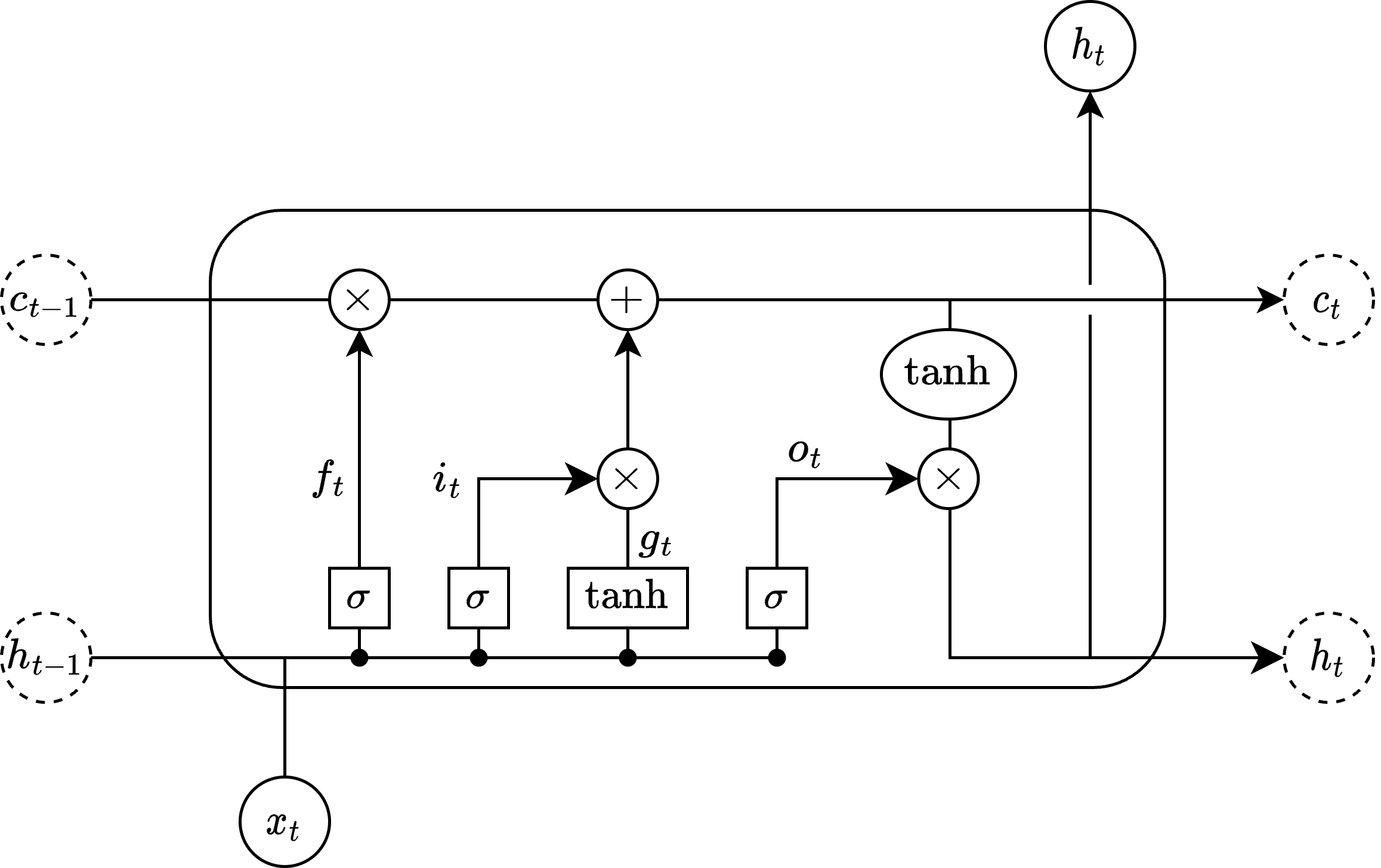
The following diagram illustrates the structure of a single LSTM cell:
The four internal activation vectors inside an LSTM cell, \(i_t\), \(f_t\), \(g_t\) and \(o_t\), are calculated using the following equations:
\[\begin{split}
\begin{align*}
i_t &= \sigma(W_{ii} x_t + b_{ii} + W_{hi} h_{t-1} + b_{hi}) \\
f_t &= \sigma(W_{if} x_t + b_{if} + W_{hf} h_{t-1} + b_{hf}) \\
g_t &= \tanh(W_{ig} x_t + b_{ig} + W_{hg} h_{t-1} + b_{hg}) \\
o_t &= \sigma(W_{io} x_t + b_{io} + W_{ho} h_{t-1} + b_{ho})
\end{align*}
\end{split}\]
x = torch.randn(d)
h0 = torch.randn(k)
c0 = torch.randn(k)
# Inpute gate's activation vector
i = sigmoid(
W_ii @ x + bias_ii + W_hi @ h0 + bias_hi
)
# Forget gate's activation vector
f = sigmoid(
W_if @ x + bias_if + W_hf @ h0 + bias_hf
)
# Cell input activation vector
g = tanh(
W_ig @ x + bias_ig + W_hg @ h0 + bias_hg
)
# Ouput gate's activation vector
o = sigmoid(
W_io @ x + bias_io + W_ho @ h0 + bias_ho
)
print(f"i: {i}")
print(f"f: {f}")
print(f"g: {g}")
print(f"o: {o}")
i: tensor([0.5944, 0.2809])
f: tensor([0.4461, 0.7488])
g: tensor([0.2927, 0.4243])
o: tensor([0.7073, 0.5732])
The cell state vector \(c_t\) and hidden state vector \(h_t\) are outputted from each LSTM cell:
\[\begin{split}
\begin{align*}
c_t &= f_t \odot c_{t-1} + i_t \odot g_t \\
h_t &= o_t \odot \tanh(c_t)
\end{align*}
\end{split}\]
# Cell state vector
c = f * c0 + i * g
# Hidden state vector, i.e.,
# output vector of the LSTM cell
h = o * tanh(c)
print(f"manual calculations of h and c:")
print(f"h: {h}")
print(f"c: {c}")
manual calculations of h and c:
h: tensor([ 0.3590, -0.3243])
c: tensor([ 0.5594, -0.6413])
with torch.no_grad():
h, c = lstm_cell(x, (h0, c0))
print(f"output from the LSTM cell:")
print(f"h: {h}")
print(f"c: {c}")
output from the LSTM cell:
h: tensor([ 0.3590, -0.3243])
c: tensor([ 0.5594, -0.6413])
As we have verified, the manual calculations agree with PyTorch’s implementation.
LSTM#
lstm = nn.LSTM(
input_size=d,
hidden_size=k,
)
lstm
LSTM(3, 2)
The state dict of an LSTM instance is different from that of an LSTM cell for LSTM may have multiple layers.
lstm.state_dict().keys()
odict_keys(['weight_ih_l0', 'weight_hh_l0', 'bias_ih_l0', 'bias_hh_l0'])
The suffix _l0 is the layer name. If we initialize an LSTM with multiple layers, then there may be l1, l2, …
For example,
nn.LSTM(
input_size=d,
hidden_size=k,
num_layers=3
).state_dict().keys()
odict_keys(['weight_ih_l0', 'weight_hh_l0', 'bias_ih_l0', 'bias_hh_l0', 'weight_ih_l1', 'weight_hh_l1', 'bias_ih_l1', 'bias_hh_l1', 'weight_ih_l2', 'weight_hh_l2', 'bias_ih_l2', 'bias_hh_l2'])
Since lstm instance has only one layer, it is essentially the same as an LSTM cell. And we can make lstm be the same as lstm_cell created previously by sharing its state dict. Of course, we must change the keys of the ordered dict.
state_dict = OrderedDict()
for key in lstm_cell.state_dict():
new_key = f"{key}_l0"
state_dict[new_key] = lstm_cell.state_dict()[key]
lstm.load_state_dict(state_dict)
<All keys matched successfully>
Suppose we have a sequence of input vectors \(x_0, x_1, \ldots, x_t\).
seq_len = 5
x_seq = torch.randn(seq_len, d)
xs = tuple(map(lambda x: x.squeeze(), x_seq.split(1)))
print("sequence as a tensor:")
print(x_seq)
print()
print("sequence as a tuple of tensors:")
pprint(xs)
sequence as a tensor:
tensor([[-0.8887, 1.2135, 0.7924],
[-0.4401, 0.4996, -0.7581],
[ 0.9989, -0.8793, 0.7486],
[-1.3375, 0.6449, 0.9652],
[ 1.0090, -0.0337, -1.0090]])
sequence as a tuple of tensors:
(tensor([-0.8887, 1.2135, 0.7924]),
tensor([-0.4401, 0.4996, -0.7581]),
tensor([ 0.9989, -0.8793, 0.7486]),
tensor([-1.3375, 0.6449, 0.9652]),
tensor([ 1.0090, -0.0337, -1.0090]))
We can feed these vectors one after another to the LSTM cell:
with torch.no_grad():
h, c = h0, c0
for x in xs:
h, c = lstm_cell(x, (h, c))
out = h
out
tensor([ 0.0362, -0.0598])
Or, equivalently we may pass the entire sequence (as a tensor) to the LSTM module:
with torch.no_grad():
out, (ht, ct) = lstm(x_seq, (h0.reshape(1, -1), c0.reshape(1, -1)))
out
tensor([[ 0.4519, -0.4052],
[ 0.0638, -0.2567],
[ 0.1473, -0.2891],
[ 0.0493, -0.1647],
[ 0.0362, -0.0598]])
Note that the output tensor out consists of all output tensors including the intermediate ones. Note also that we have reshaped the initial hidden and cell state vectors before passing to LSTM. Again, this is because LSTM may have multiple layers. The first of reshape is set 1 because there is only one layer.
To obtain the last output vector, as are usually of interest, we simply access via last index out[-1]. Alternatively, we may use ht since they are the same.
print(f"last output vector from LSTM:\n{out[-1]}")
print()
print(f"last hidden state vector:\n{ht}")
last output vector from LSTM:
tensor([ 0.0362, -0.0598])
last hidden state vector:
tensor([[ 0.0362, -0.0598]])
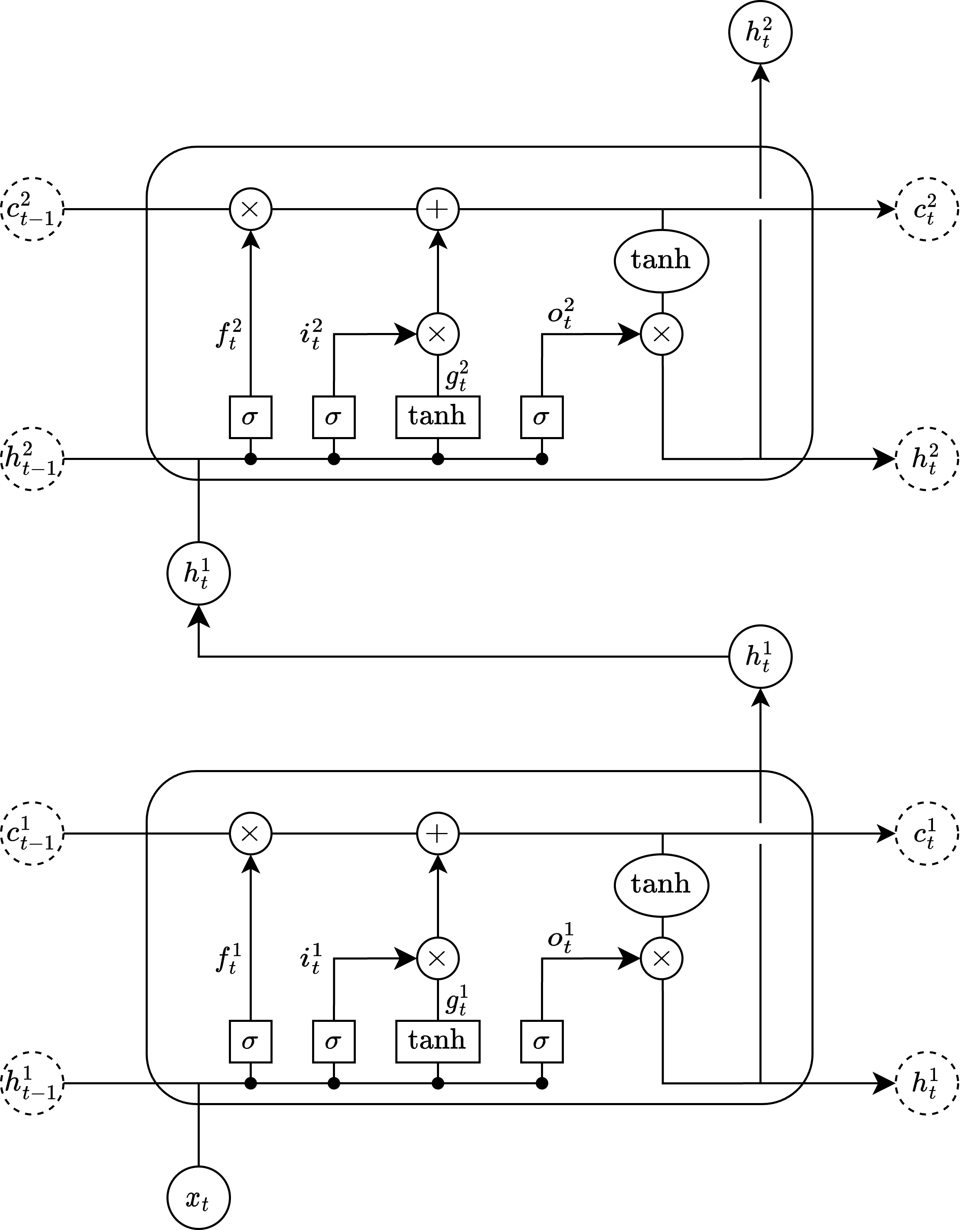
Stacked LSTM#
stacked_lstm = nn.LSTM(
input_size=d,
hidden_size=k,
num_layers=2
)
stacked_lstm
LSTM(3, 2, num_layers=2)
The structure of this stacked LSTM is as follows:
lstm_cell1 = nn.LSTMCell(
input_size=d,
hidden_size=k
)
lstm_cell2 = nn.LSTMCell(
input_size=k,
hidden_size=k
)
state_dict = OrderedDict()
for key in lstm_cell1.state_dict():
new_key = f"{key}_l0"
state_dict[new_key] = lstm_cell1.state_dict()[key]
for key in lstm_cell2.state_dict():
new_key = f"{key}_l1"
state_dict[new_key] = lstm_cell2.state_dict()[key]
stacked_lstm.load_state_dict(state_dict)
<All keys matched successfully>
with torch.no_grad():
h_cell1, c_cell1 = h0, c0
h_cell2, c_cell2 = h0, c0
for x in xs:
h_cell1, c_cell1 = lstm_cell1(x, (h_cell1, c_cell1))
h_cell2, c_cell2 = lstm_cell2(h_cell1, (h_cell2, c_cell2))
out = h_cell2
out
tensor([ 0.1681, -0.0548])
with torch.no_grad():
out, (ht, ct) = stacked_lstm(
x_seq,
(
h0.repeat(2).reshape(2, -1),
c0.repeat(2).reshape(2, -1)
)
)
out
tensor([[ 0.2394, -0.1301],
[ 0.1795, -0.1011],
[ 0.1759, -0.0746],
[ 0.1596, -0.0619],
[ 0.1681, -0.0548]])
ht
tensor([[ 0.1617, -0.0132],
[ 0.1681, -0.0548]])
h_cell1
tensor([ 0.1617, -0.0132])
h_cell2
tensor([ 0.1681, -0.0548])
Air Quality Prediction Using LSTM#
Data#
# Read original CSV file content
with open("../data/air-quality/AirQualityUCI.csv", "r") as f:
air_quality_file_content = f.read()
# Clean the file content
air_quality_file_content = air_quality_file_content.replace(",", ".").replace(";", ",")
air_quality_str_io = StringIO(air_quality_file_content)
air_quality = pd.read_csv(air_quality_str_io)
# Drop empty columns, and then
# drop empty rows
air_quality = air_quality.dropna(axis=1, how="all").dropna(axis=0, how="all")
air_quality
original_to_revised_column_name = {
"CO(GT)": "co",
"NO2(GT)": "no2",
"T": "temperature",
"RH": "relative_humidity",
"AH": "absolute_humidity"
}
air_quality: pd.DataFrame = air_quality.loc[:, original_to_revised_column_name.keys()]
air_quality.rename(columns=original_to_revised_column_name, inplace=True)
air_quality
class SlidingWindowSplitter(BaseEstimator, TransformerMixin):
def __init__(
self,
lookback: int = 1,
forward_horizon: int = 1
) -> None:
super().__init__()
self.lookback = lookback
self.forward_horizon = forward_horizon
def fit(
self,
seq: np.ndarray,
target_seq: Optional[np.ndarray] = None,
) -> Self:
return self
def transform(
self,
seq: np.ndarray,
target_seq: Optional[np.ndarray] = None,
) -> tuple[np.ndarray, np.ndarray]:
total_seq_length = seq.shape[0]
if target_seq is not None:
assert target_seq.shape[0] == total_seq_length
rows = []
target_rows = []
window_size = self.lookback + self.forward_horizon
for i in range(total_seq_length - (window_size - 1)):
rows.append(seq[i:i+window_size].copy())
if target_seq is not None:
target_rows.append(target_seq[i:i+window_size].copy())
# Convert to an array
rows = np.stack(rows)
if target_seq is not None:
target_rows = np.stack(target_rows)
if target_seq is None:
X = rows[:, :self.lookback]
y = rows[:, self.lookback:]
else:
X = rows[:, :self.lookback]
y = target_rows[:, self.lookback:]
return X, y
sliding_window_splitter = SlidingWindowSplitter(lookback=3, forward_horizon=1)
X, y = sliding_window_splitter.fit_transform(
air_quality.to_numpy(),
target_seq=air_quality.loc[:, ["co", "no2"]].to_numpy(),
)
X.shape, y.shape